3 Voorstelling van de gegevens

3.1 Onzekerheid

Alle resultaten zijn gebaseerd op een steekproef en op de waarnemingen zit onvermijdelijk een zekere meetfout. Vandaar dat we bij de puntschattingen tevens een betrouwbaarheidsinterval weergeven. In de tekst gebruiken we het 90% (5%; 95%) interval waarbij er 5% kans is dat de werkelijke waarde kleiner is dan de ondergrens en 5% dat ze groter is dan de bovengrens. Het 90% interval is iets smaller dan het traditionele 95% (2.5%; 97.5%) interval. Door een smaller interval te kiezen zullen we sneller uitspraken kunnen doen, waardoor de kans kleiner wordt dat we ten onrechte stellen dat er geen effect is. De prijs die we hiervoor betalen is dat de kans dat we ten onrechte stellen dat er een significant effect is, stijgt van 5% naar 10%. De doelstelling van de algemene broedvogelmonitoring is zo spoedig mogelijk detecteren wanneer er iets aan de hand is de broedvogels. Vanuit dat oogpunt is het vermijden van vals negatieve signalen (ten onrechte stellen dat er niets aan de hand is) belangrijker dan het vermijden van vals positieve signalen (ten onrechte stellen dat er iets aan de hand is).

Wanneer we het interval op een figuur (bijvoorbeeld fig. 3.1) weergeven, vullen we het 90% interval aan met een 60% (20%; 80%) interval en een 30% (35%; 65%) interval. Britton et al. (1998) waren de inspiratie voor deze manier van weergeven. Het 30% interval vormt het donkerste deel van het interval en geeft de meeste waarschijnlijke locatie van de werkelijke waarde weer. Naarmate het interval lichter wordt, neemt de onzekerheid toe.

3.2 Opdeling van de effecten in een aantal klassen

Bij het niet-lineaire model berekenen we alle paarsgewijze relatieve verschillen tussen de verschillende jaren. Bij het lineaire model hebben we de gemiddelde jaarlijkse relatieve verandering. Deze laatste rekenen we tevens om naar de totale wijziging over de looptijd van het meetnet omdat dit eenvoudiger te interpreteren is. Vergelijk een daling met -5% per jaar of een daling met -50% over 15 jaar. Deze laatste klinkt dramatischer door het grotere cijfer, terwijl -5% per jaar overeenkomt met -54% over 15 jaar. De totale wijziging over de looptijd van het lineaire model is tevens vergelijkbaar met de wijziging tussen het eerste en laatste jaar van het niet-lineaire model.

Om de interpretatie makkelijker te maken, delen we de wijzigingen op in tien klassen door hun 90% interval te vergelijken met een referentie, ondergrens en bovengrens. Een effect is significant wanneer de referentie buiten het 90% interval ligt. We spreken over een toename (afname) als het interval volledig boven (onder) de referentie ligt. Niet significante effect is ook informatief wanneer het bijhorende interval voldoende smal is. Bijvoorbeeld als het interval volledig tussen de ondergrens en bovengrens ligt. In dat geval kunnen we stellen dat het effect niet significant en klein is, het immers zeker minder sterk dan de ondergrens en minder sterk dan de bovengrens. Dergelijk effect krijgt de naam stabiel. Heeft het effect een breed interval dat zowel de boven- als ondergrens bevat, spreken we over een onduidelijk effect. Daarnaast is er nog de mogelijkheid dat het interval zowel de bovengrens (ondergrens) als de referentie bevat maar niet de ondergrens (bovengrens). Dan spreken we over een mogelijke toename (mogelijke afname). We kunnen de boven- en ondergrens eveneens gebruiken om een verder onderscheid te maken binnen de significante effecten. Een interval volledig boven (onder) de bovengrens (ondergrens) wordt dan een sterke toename (sterke afname). Een interval volledig tussen de referentie en de de bovengrens (ondergrens) wordt dan een matige toename (matige afname). Een interval dat de referentie niet bevat maar wel de bovengrens (ondergrens) blijft een toename (afname). Merk op dat de indeling volledig gebaseerd is op de onzekerheid rond het effect en niet op de puntschatting van het effect zelf. We vatten de opdeling met bijhorende afkortingen en regels samen in tabel 3.1. Figuur 3.1 geeft een grafische voorstelling waarbij we de afkortingen in combinatie met aangepaste symbolen gebruiken. De afkortingen zelf zijn te fijn om als symbool te gebruiken.

Tabel 3.1: Overzicht van de benamingen van de tien effectklassen met hun afkorting en de regels. \(R\): referentie, \(L\): ondergrens, \(B\): bovengrens, \(l\): ondergrens van het 90% interval, \(b\): bovengrens van het 90% interval. \(L < R < B\) en \(l < b\).
benaming afkorting regels
sterke toename ++ \(B < l\)
toename + \(R < l < B\) en \(B < b\)
matige toename +~ \(R < l < B\) en \(b < B\)
stabiel ~ \(L < l < R\) en \(R < b < B\)
matige afname -~ \(L < l < R\) en \(b < R\)
afname - \(l < L\) en \(L < b < R\)
sterke afname -- \(l < L\)
mogelijke toename ?+ \(L < l < R\) en \(B < b\)
mogelijke afname ?- \(l < L\) en \(R < b < B\)
onduidelijk ? \(l < L\) en \(B < b\)
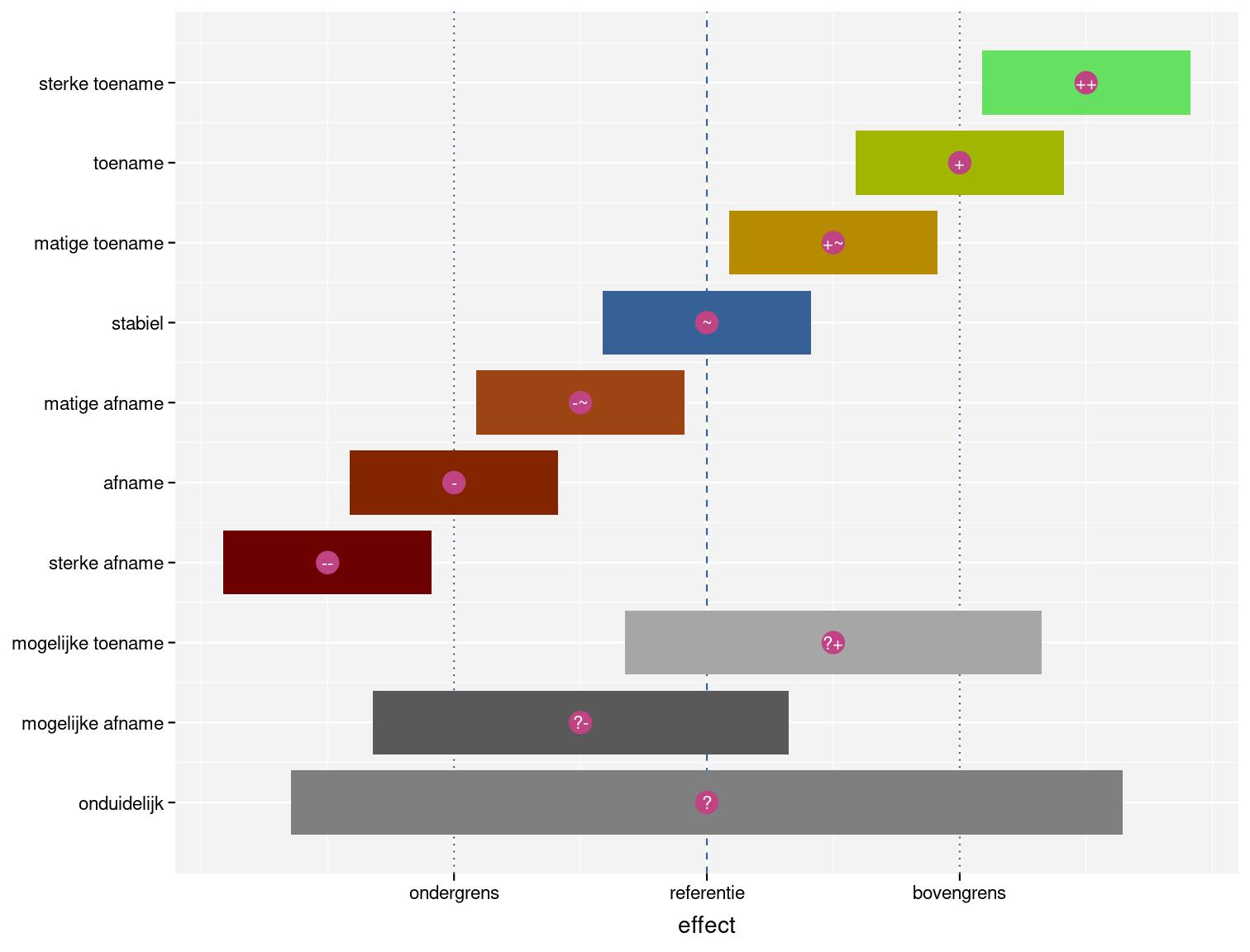
Voorbeeld van de tien mogelijke interpretaties van een effect door het 90% interval te vergelijken met een referentie, ondergrens en bovengrens.

Figuur 3.1: Voorbeeld van de tien mogelijke interpretaties van een effect door het 90% interval te vergelijken met een referentie, ondergrens en bovengrens.

Uiteraard hangt de opdeling sterk af van de keuze van de boven- en ondergrens. De soortenmeetnetten voor de Natura 2000 monitoring streven er naar om een daling in populatiegrootte met -25% over 25 jaar tijd vast te kunnen stellen. Hierbij wordt een wijziging in de populatiegrootte van -25% als belangrijk aanzien. Daarom hanteren we voor de algemene broedvogelmonitoring ook -25% als ondergrens, zowel bij de paarsgewijze verschillen tussen de jaren als de lineaire wijziging over de looptijd van het meetnet. Een van daling van -25% komt overeen met aantallen die nog drie kwart van de uitgangssituatie bedragen. Een even sterke wijziging in de omgekeerde richting zorgt er voor dat de aantallen toenemen tot vier derde van de uitgangssituatie, of een toename met +33% wat we als bovengrens gebruiken.

Bij de samengestelde indices hebben we aangepaste grenswaarden nodig. Veronderstel een samengestelde index op basis van \(n\) soorten. We berekenen het rekenkundig gemiddelde in de log-schaal, dan is de variantie van dit gemiddelde een factor \(n\) kleiner dan de som van de varianties. De breedte van een betrouwbaarheidsinterval hangt samen met de standaard afwijking, wat de vierkantswortel van de variantie is. Hierdoor zullen de breedtes van de betrouwbaarheidsintervallen van de samengestelde index een factor \(\sqrt{n}\) kleiner zijn. Vandaar dat we de grenswaarden van de indices tevens aanpassen door ze met een factor \(\sqrt{n}\) te verkleinen. Elke samengestelde index heeft zijn eigen soortenlijst met een variabele aantal soorten. Daarom zullen we bij elke samengestelde index zijn aangepaste grenswaarden vermelden.

3.4 Evolutie van gemiddelde aantallen per soort

Deze figuur geeft de evolutie van de gemiddelde aantallen per meetpunt weer volgens het niet-lineair model. Indien het model lineair is, zal het patroon van de niet-lineaire trend dicht bij een lineaire trend liggen. De lijn bevat de puntschatting van het gemiddelde aantal in elk jaar. Rond de lijn tonen we het 30%, 60% en 90% interval (zie §3.1). In de online versie van het rapport is de figuur interactief. Wanneer de gebruiker met de muis over de figuur gaat verschijnt er in de buurt van de lijn een pop-up met de exacte schatting van dat jaar inclusief het 90% betrouwbaarheidsinterval en het jaartal.

3.5 Paarsgewijze vergelijking van jaren

Deze informatie hebben we telkens in twee figuren samengevat. De eerste figuur geeft het verschil van elk jaar t.o.v. 2007, het jaar waarin de metingen gestart zijn. Voor 2007 geven we geen cijfer omdat het per definitie 1 is en geen informatie bevat. Het symbool geeft de puntschatting van het relatieve verschil t.o.v. 2007 weer. De vorm van het symbool geeft de opdeling van de sterkte van het effect weer (zie fig. 3.1). Rond elke puntschatting tonen we het 30%, 60% en 90% interval (zie §3.1). De horizontale streepjeslijn geeft de referentie van 0% verschil weer. De horizontale puntlijnen geven de bovengrens (+33%) en ondergrens (-25%) weer. Deze laten toe om de vlot zelf de betrouwbaarheidsintervallen te vergelijken met de referentie, boven- en ondergrens. De figuur heeft twee y-assen. Beide assen geven dezelfde informatie weer, enkel de formattering van de labels is anders. De linkeras toont procentuele verschillen terwijl de rechteras de relatieve verschillen toont. Een procentueel verschil van +50% is equivalent met een relatieve verschil (verhouding) met een factor 1,5.

We stellen vast dat veel gebruikers ook andere jaren met elkaar willen vergelijken. Een correcte vergelijking is enkel mogelijk indien we een van deze jaren als referentie gebruiken. Voor elk jaar een afzonderlijke figuur maken, zou het rapport onoverzichtelijk groot maken. Om de vergelijkingen toch mogelijk te maken hebben we alle paarsgewijze verschillen tussen de jaren in een raster weergeven. Elke rij in het raster staat voor een ander referentiejaar. De kolommen geven de verschillen van een bepaald jaar weer t.o.v. de verschillende referentiejaren. Op de diagonaal staan geen waarden omdat we daar een jaar met zichzelf vergelijken. De kleur van de symbolen geeft de sterkte van het verschil (gebaseerd op de puntschatting). Zwakke verschillen zijn grijs, sterke positieve verschillen rood, sterke negatieve verschillen blauw. De vorm van de symbolen geeft zicht op de sterkte en onzekerheid van het effect (zie tab. 3.1). Wanneer een rij volledig rood (blauw) is, zijn alle verschillen met dit referentiejaar positief (negatief) m.a.w. dit is het referentiejaar met de laagste (hoogste) aantallen. Wanneer een kolom volledig rood (blauw) is, zijn alle verschillen van dit jaar t.o.v. alle referentiejaren negatief (positief) m.a.w. dit is het jaar met de hoogste (laagste) aantallen. Clusters van punten met een gelijkaardige kleur geven periodes aan waarin de aantallen geleidelijk wijzigen. In de online versie van dit rapport is deze figuur interactief. Wanneer de gebruiker met de muis over de figuur gaat verschijnt er in de buurt van de lijn een pop-up met de exacte schatting van dat punt inclusief het 90% betrouwbaarheidsinterval en het jaartal en referentiejaar.

Referenties

Britton E., Fisher P. & Whitley J. (1998). The Inflation Report Projections: Understanding the Fan Chart. Bank of England Quarterly Bulletin 30–37.

 

Creative Commons-Licentie Onkelinx, T.; Vermeersch, G. & Devos, K. (2023). 10.21436/inbor.89419879