C Appendix: Aantal en oppervlakte op te volgen locaties bepalen

C.1 Algemeen

Uit analyse van de natuurdoelenkaart, blijkt dat een natuurstreefbeeld in een gebied een gemiddelde habitatvlek-oppervlakte kan hebben tot 45 ha en de grootste habitatvlekken zijn ongeveer 100 ha. Daar staat tegenover dat de helft van de habitatvlekken minder dan 0.28 ha groot zijn. Het aantal beheereenheden van een natuurstreefbeeld kan in een bepaald gebied oplopen tot 375, maar in de helft van de gevallen is dit minder dan 20. Een andere vaststelling is dat er een omgekeerd evenredige relatie is tussen het aantal habitatvlekken en de gemiddelde oppervlakte ervan omwille van de eindige totale oppervlakte van een gebied.

Deze grote variatie tussen gebieden aan oppervlaktes van individuele habitatvlekken en aantallen habitatvlekken per natuurstreefbeeld, vereist dat we een methodiek moeten hebben die bij zeer grote en/of versnipperde gebieden toelaat om de inspanning te beperken tot iets wat haalbaar is en toch voldoende gegevens oplevert voor een evaluatie. We vertrekken voor de berekening van het aantal op te volgen locaties daarom van de totale oppervlakte van een natuurstreefbeeld tot doel gesteld in een gebied om het aantal op te volgen locaties te bepalen. Zo’n totale oppervlakte kan dus zowel het resultaat zijn van weinig habitatvlekken met een relatief grote gemiddelde oppervlakte, of veel habitatvlekken met een relatief kleine gemiddelde oppervlakte.

Uit Figuur C.1 en Figuur C.2 kan afgeleid worden hoeveel locaties opgevolgd moeten worden (dit is te beschouwen als de gevraagde minimuminspanning om voor subsidies in aanmerking te komen). Dit aantal is afhankelijk van de oppervlakte tot doel gesteld voor een bepaald natuurstreefbeeld. Verderop geven we bijkomende richtlijnen om de oppervlakte van een opname te bepalen. We veronderstellen bij de berekening van het aantal op te volgen locaties dat wanneer de oppervlakte zeer groot is, we voldoende hebben aan een beoordeling van het terrein op 50 locaties.1

In realiteit is de oppervlakte meestal beperkt. Daarom werd een correctie gemaakt die het aantal op te volgen locaties naar beneden corrigeert (de curves zijn berekend met behulp van een eindige populatie correctiefactor, zie bv. Elzinga et al. (2001)). In plaats van de curves te bekijken, kan het aantal op te volgen locaties ook als volgt berekend worden (mits afronding van het resultaat naar boven):

\[n = \frac{50}{1 + 50/N}\]

Waarbij \(N\) de totale oppervlakte tot doel gesteld in hectare.

Deze berekeningen moeten beschouwd worden als de minimuminspanning die gevraagd wordt. Een beheerder mag altijd meer doen dan wat gevraagd wordt. De berekening is vooral bedoeld om te vermijden dat bij grote oppervlaktes natuurstreefbeeld alles zou moeten opgevolgd worden. Een beheerder die 500 ha heide beheert, wil waarschijnlijk vooral een signaal te krijgen als het minder goed gaat en hij moet ingrijpen. Bij kleine oppervlakte van een natuurstreefbeeld daarentegen, wil een beheerder in principe weten wat de toestand is in elke beheereenheid. Voor kleinere oppervlaktes geeft de formule daarom aan dat een relatief groter aandeel zal opgevolgd worden (in absolute termen wordt minder opgevolgd, maar relatief gezien meer). Dit is in de veronderstelling dat het natuurstreefbeeld niet versnipperd is over veel meer beheereenheden dan de oppervlakte ervan uitgedrukt in hectare.

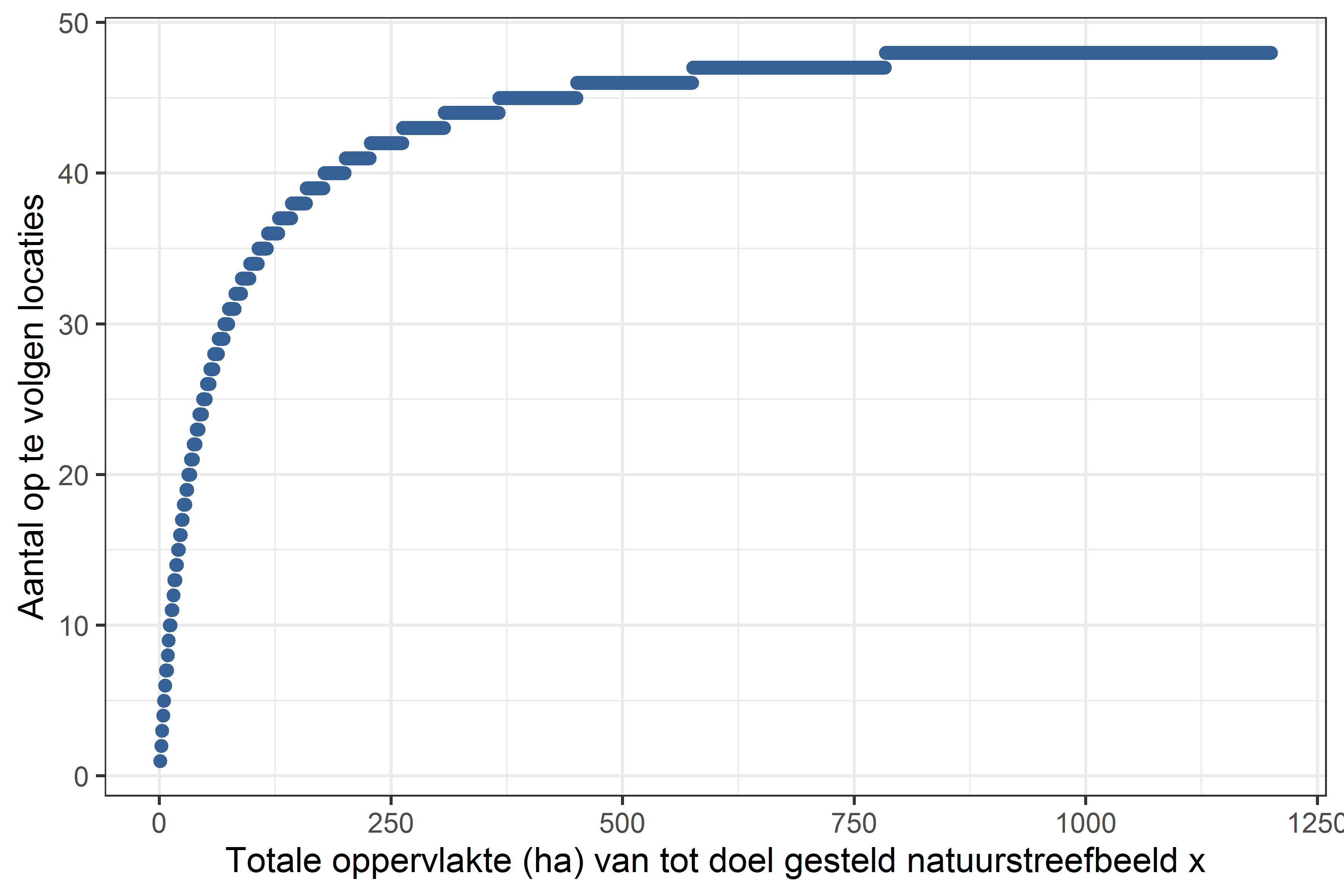
Eeste stap in het bepalen van het aantal op te volgen locaties. De totale oppervlakte bepaalt voor een natuurstreefbeeld het aantal op te volgen locaties.

Figuur C.1: Eeste stap in het bepalen van het aantal op te volgen locaties. De totale oppervlakte bepaalt voor een natuurstreefbeeld het aantal op te volgen locaties.

Zelfde als Figuur C.1, maar ingezoomd zodat beter de waarden bij kleinere oppervlaktes kunnen afgelezen worden. De rode lijnen geven een voorbeeld: een totale oppervlakte van 20 ha stemt overeen met 15 op te volgen locaties.

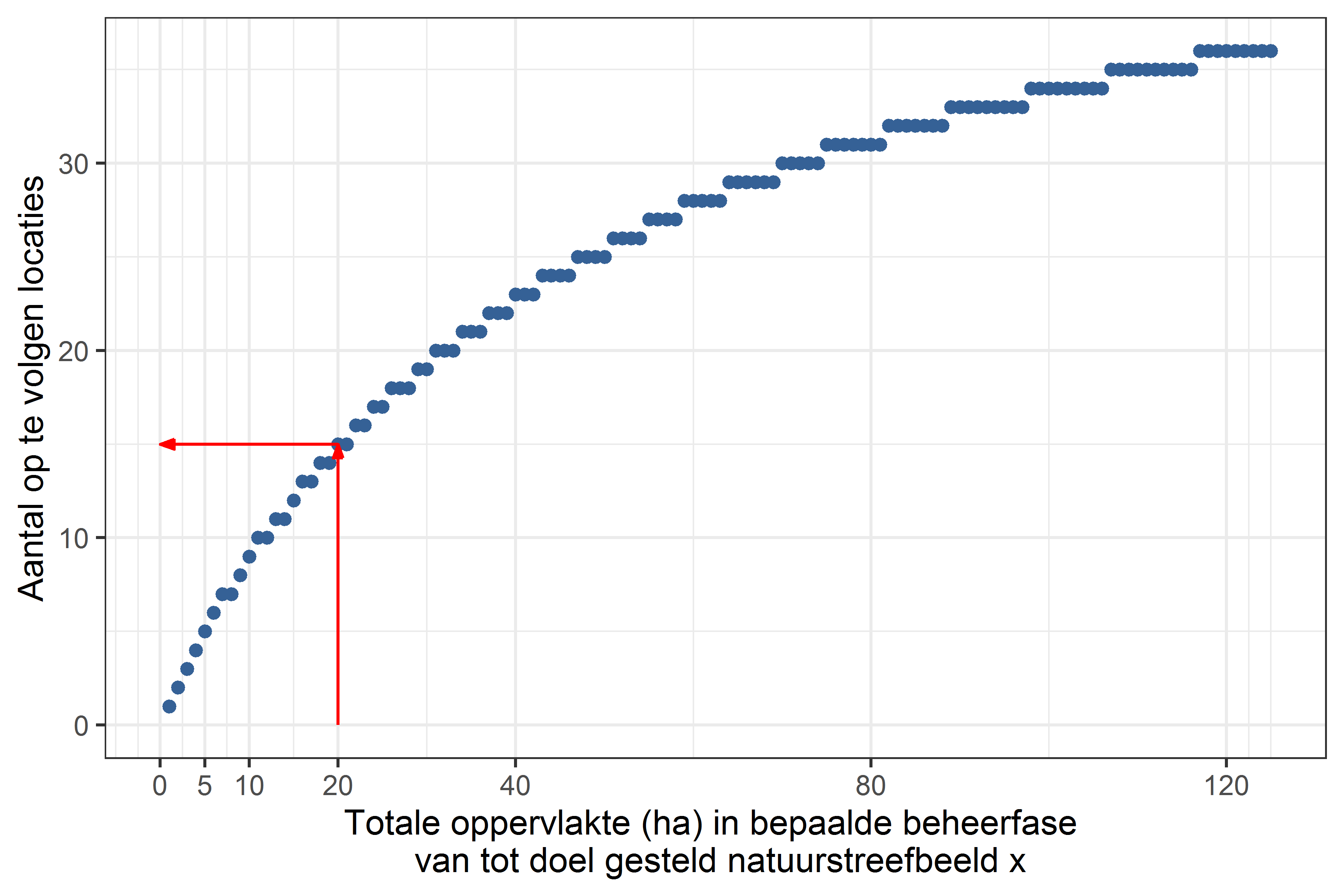
Figuur C.2: Zelfde als Figuur C.1, maar ingezoomd zodat beter de waarden bij kleinere oppervlaktes kunnen afgelezen worden. De rode lijnen geven een voorbeeld: een totale oppervlakte van 20 ha stemt overeen met 15 op te volgen locaties.

De totale oppervlakte wordt bepaald door het aantal beheereenheden en de gemiddelde grootte ervan. Op basis van de eerder vastgestelde mogelijke combinaties uit de habitatdoelenkaart, kunnen we via Figuur C.3 ook het aantal op te volgen locaties aflezen.

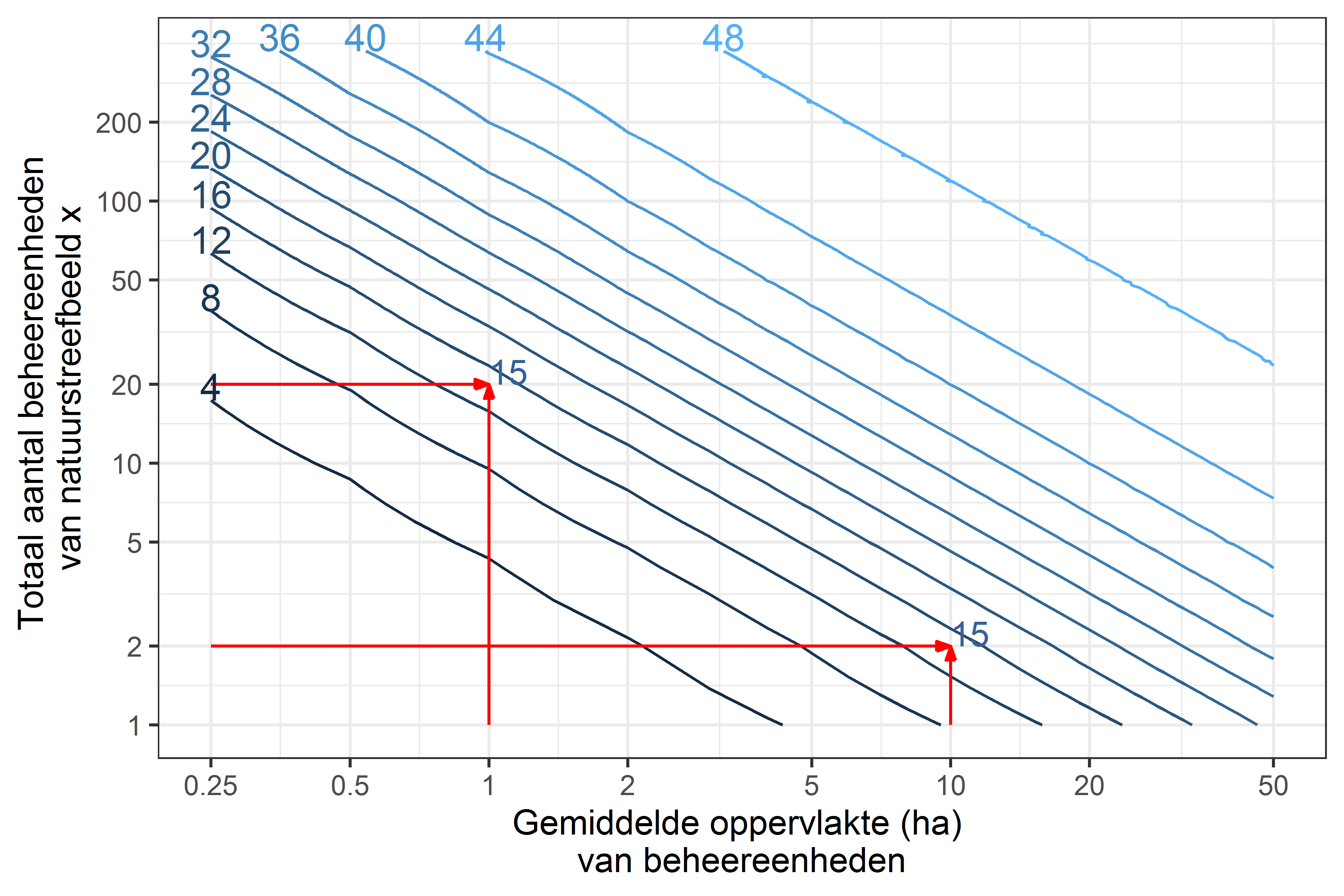
Aantal op te volgen locaties in functie van het aantal beheereenheden (habitatvlekken) en de gemiddelde oppervlakte ervan. De maximale waarden langs de assen zijn bepaald op basis van alle vastgestelde combinaties in de natuurdoelenkaart. De rode lijnen herhalen het voorbeeld van Figuur C.2 en tonen hoe een totale oppervlakte van 20 ha zowel het resultaat kan zijn van vele kleine beheereenheden als weinig grote beheereenheden.

Figuur C.3: Aantal op te volgen locaties in functie van het aantal beheereenheden (habitatvlekken) en de gemiddelde oppervlakte ervan. De maximale waarden langs de assen zijn bepaald op basis van alle vastgestelde combinaties in de natuurdoelenkaart. De rode lijnen herhalen het voorbeeld van Figuur C.2 en tonen hoe een totale oppervlakte van 20 ha zowel het resultaat kan zijn van vele kleine beheereenheden als weinig grote beheereenheden.

Voor elk van de natuurstreefbeelden is er een maximale oppervlakte van een habitatvlek in een beheereenheid waarover een opname kan gemaakt worden en een aanbevolen oppervlakte. De aanbevolen en grootte van een proefvlak is voor de meeste vegetaties 0,5 ha, en de maximale oppervlakte die in één keer kan beoordeeld worden is 1 ha. Voor een aantal vegetatietypes gelden andere waarden. Deze zijn opgenomen in Tabel C.1). Voor oevervegetaties werd oppervlakte omgezet naar oeverlengte. Voor habitatvlekken die groter zijn dan de maximum oppervlakte wordt een locatie binnen de vlek opgevolgd met oppervlakte gelijk aan de aanbevolen oppervlakte.

Tabel C.1: Overzicht van natuurstreefbeelden waarvoor de maximum en aanbevolen oppervlakte of perimeter afwijkt van de standaard (standaard: maximum = 1 ha en aanbevolen = 0,5 ha). De kolom ‘Maximum’ geeft de maximale oppervlakte of lengte die in één keer kan beoordeeld worden (één opname). De kolom ‘Aanbevolen’ geeft de aanbevolen oppervlakte of lengte van een locatie (indien de habitatvlek groter is dan ‘Maximum’.
HAB Maximum Aanbevolen Eenheid
1130 2 1 ha
2130_hd 2 1 ha
2180 2 1 ha
2310 2 1 ha
2330 2 1 ha
2330_bu 2 1 ha
2330_dw 2 1 ha
4030 2 1 ha
rbbah 2 1 ha
rbbkam 2 1 ha
rbbppm 2 1 ha
3130 400 100 m
3130_aom 400 100 m
3150 400 100 m
3160 400 100 m
3140 500 100 m

De maximum-oppervlakte (\(a_{max}\)) is de oppervlakte waarover een beheereenheid (of de zone binnen de beheereenheid waar het natuurstreefbeeld tot doel is gesteld indien het een beheereenheid betreft die om pragmatische redenen meerdere natuurstreefbeelden omvat) in zijn geheel kan opgevolgd worden (1 opname). Deze oppervlakte is afhankelijk van het natuurstreefbeeld (soortenrijkdom, structuurvariatie kunnen inschatten, …). Wanneer een beheereenheid groter is dan \(a_{max}\), wordt deze onoverzichtelijk en wordt de inschattingsfout te groot. Het zou bovendien te lang duren om een goed beeld te krijgen van het terrein. Wanneer de beheereenheid (of de habitatvlek(ken) erbinnen) (veel) groter is dan deze maximum oppervlakte, worden inschattingen gemaakt in één of meerdere proefvlakken. Van zodra er meerdere proefvlakken binnen eenzelfde beheereenheid bekeken worden (herhalingen), mag de oppervlakte van zo’n individuele herhaling verkleinen. Er kan immers een voldoende representatief beeld van het terrein bekomen worden met opnamen over een kleinere oppervlakte naarmate het aantal replicas (locaties) binnen dezelfde beheereenheid stijgt.

In tabel C.2 geven we de aangewezen proefvlakoppervlaktes in functie van het aantal herhalingen en de aanbevolen oppervlakte zonder herhalingen voor een vegetatie-natuurstreefbeeld. We geven ook de overeenkomstige straal en zijde in geval van, respectievelijk een proefvlakcirkel en een proefvlakvierkant. Het gaat in totaal over vijf mogelijke proefvlakoppervlaktes (1 ha, 1/2 ha, 1/4 ha, 1/8 ha, 1/16 ha). Na vereenvoudiging en afronding volgt dit ongeveer de oppervlakte bekomen door deling van de aanbevolen oppervlakte door de vierkantswortel van het aantal herhalingen (= aantal locaties binnen dezelfde beheereenheid) (\(r\)): \(a_{aanb} / \sqrt{r})\). Hierdoor neemt de totale oppervlakte die bekeken wordt binnen de beheereenheid (\(r * a_{aanb} / \sqrt{r}\)) traag toe ten opzichte van \(a_{aanb}\), zodat een redelijk deel van het terrein bekeken wordt (verhoogde trefkans voor iets zeldzamere soorten). Stel dat een natuurstreefbeeld in één beheereenheid van 50 ha voorkomt, dan zouden we dus \(r = 50/(1 + 50/50) = 25\), en bij \(a_{aanb} = 0.5 ha\) net 5% van deze oppervlakte bekijken: \(25 * 0.5 / sqrt(25) = 25 * 0.1 = 2.5 ha\) (zie ook voorbeeld 1 hieronder).

Tabel C.2: De vijf mogelijke oppervlaktes van een proefvlak (in ha) en hun overeenkomstige afmetingen in geval van een proefvlakcirkel (straal in meter) of een vierkant proefvlak (zijde in meter) afgerond op 5m nauwkeurigheid. De proefvlakoppervlakte is afhankelijk van het aantal herhalingen en de aanbevolen oppervlakte van een proefvlak zonder herhalingen in een beheereenheid voor een vegetatie-natuurstreefbeeld.
Proefvlakoppervlakte (ha) indien geen herhaling Aantal herhalingen Proefvlakoppervlakte (ha) bij r herhalingen Straal (m) Zijde (m)
0.5 1-2 0.5000 40 70
0.5 3-7 0.2500 30 50
0.5 8-32 0.1250 20 35
0.5 33-50 0.0625 15 25
1.0 1-2 1.0000 55 100
1.0 3-7 0.5000 40 70
1.0 8-32 0.2500 30 50
1.0 33-50 0.1250 20 35

Bij de opvolging van de resultaten van het beheer, passen we de beheermonitoringsschaal dus toe over vrij grote oppervlaktes (van meerdere are tot maximum twee ha; in elk geval vaak groter dan traditionele proefvlakgroottes). Wanneer we slechts één opname maken (één beheereenheid), dan is het voor beheermonitoring van groot belang dat we een goed beeld krijgen van het volledige of toch een groot deel van het terrein. Indien we een te klein deel van het terrein zouden kiezen (in het geval van één opname) zouden toevalsfactoren en oppervlakte-effecten te veel spelen (door toeval ligt de opname bijvoorbeeld in het best ontwikkelde deel van het terrein en door de kleine oppervlakte vallen verschillende indicatorsoorten toch buiten de opname). Het gebrek aan replicatie wordt dus gecompenseerd doordat we een inschatting hebben voor alle gedetecteerde soorten. Deze kunnen we vervolgens aggregeren (uitmiddelen, sommeren) om een signaal te krijgen voor bv vergrassing, bedekking sleutelsoorten, …

In de omvormingsfase, herstelfase of overgangsfase, worden de locaties best representatief gekozen voor de beheervragen die zich stellen (bv in het minst goed ontwikkelde deel van het terrein waar de meeste twijfels zijn). In de instandhoudingsfase mag de locatie bv het centrum van de beheereenheid zijn of, indien het meerdere locaties betreft, goed ruimtelijk gespreid over de beheereenheid. Indien er echter drukken of bedreigingen zijn waarvan geweten is uit welke richting ze komen, dan is het raadzamer om de locatie dicht bij deze drukken of bedreigingen te nemen zodat eventuele tekenen van degradatie sneller worden gesignaleerd.

C.2 Samengevat in een stappenplan

  1. Bepaal voor een natuurstreefbeeld \(n\): Figuur C.1, Figuur C.2 en Figuur C.3)
  2. Wat zijn de belangrijkste beheervragen bij ontwikkeling of herstel en externe drukken en bedreigingen bij instandhouding? Welke beheereenheden en plaatsen binnen de beheereenheden worden in functie daarvan best opgevolgd?
  3. Afhankelijk van de oppervlakte van de beheereenheid, of het deel ervan waar het natuurstreefbeeld op van toepassing is, (\(a\) in hectare):
    • maak je een opname over de gehele beheereenheid indien deze kleiner is dan de maximale oppervlakte zoals vermeld in Tabel C.1
    • in het andere geval maak je een opname in proefvlakken waarbij de grootte van het proefvlak afhankelijk is van het aantal herhalingen en kan afgelezen worden uit Tabel C.2
  4. De effectief opgevolgde oppervlakte is dan de som van de respectievelijke bekeken oppervlaktes (\(a_i\) voor elke beheereenheid \(i\) met \(a_i \leq a_{max}\) en \(\frac{a_{aanb}}{\sqrt{r_j}}\) voor elk van \(r_j\) locaties binnen elke beheereenheid \(j\) met \(a_j > a_{max}\) )

C.3 Aanpak voor mozaïekvegetaties

De oppervlakte van de mozaïekvegetaties wordt als geheel beschouwd om de aantallen locaties te berekenen en het standaard maximum aantal op te volgen locaties wordt eveneens op 50 gezet (zie Figuur C.4). Ook wordt hier standaard een zesjaarlijkse cyclus (dus geen onderscheid tussen herstel en instandhouding) verondersteld. Binnen dit geheel, zullen dus gewoonlijk meerdere locaties (r replicaties) worden opgevolgd met een compilatielijst (bv in een mozaïekvegetatie van 50 ha in één beheerblok zullen 25 locaties opgevolgd worden. Voor de oppervlakte van een opname op één van de locaties neemt men de oppervlakte die dichtst aansluit bij de reeks in Tabel C.2 en zoals weergegeven in Figuur C.4. In het geval van mozaïekvegetaties mag de “aanbevolen oppervlakte” (zie bijlage 4) standaard gelijkgesteld worden aan 1 ha.

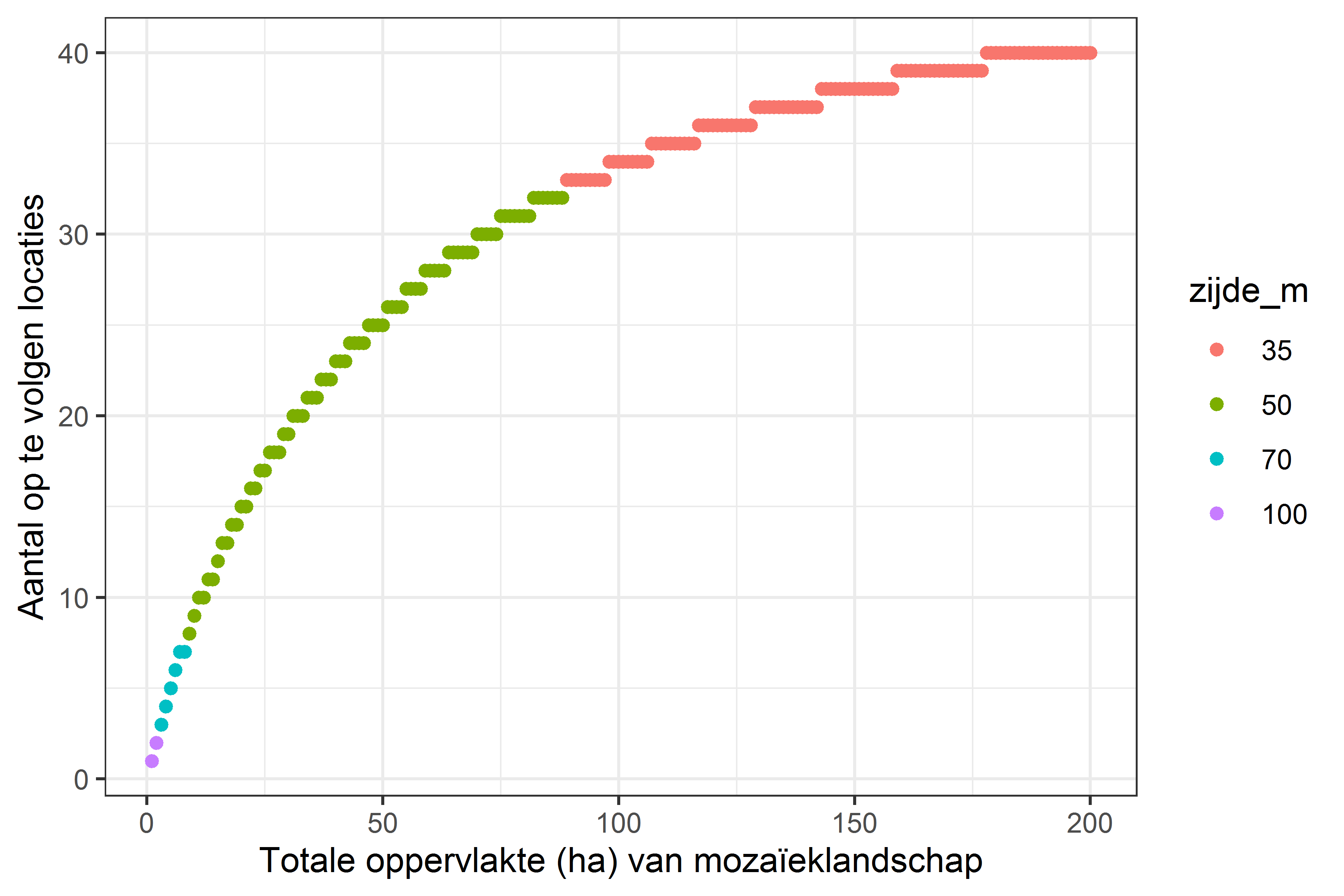
Aantal op te volgen locaties in geval van mozaïeklandschappen. De kleurgradiënt geeft aan welke afmeting mag gebruikt worden als zijde van een vierkant proefvlak.

Figuur C.4: Aantal op te volgen locaties in geval van mozaïeklandschappen. De kleurgradiënt geeft aan welke afmeting mag gebruikt worden als zijde van een vierkant proefvlak.

C.4 Voorbeelden hoe het aantal op te volgen locaties te verdelen over de beheereenheden

voorbeeld 1: er is één beheereenheid van 10 ha met natuurstreefbeeld 6510_hu

  1. \(n = 9\)
  2. Bij gebrek aan een duidelijke beheervraag is de beste strategie een goede ruimtelijke spreiding van de locaties over de beheereenheid (bv langs transecten of een grid)
  3. De oppervlakte van de enige beheereenheid is groter dan \(a_{max} = 1\), dus we nemen \(r = n\)
  4. Binnen deze beheereenheid corrigeren we de aanbevolen oppervlakte voor het type (\(a_{aanb} = 0.5\)) naar beneden omdat al deze locaties binnen dezelfde beheereenheid liggen (zie tabel C.2): \(1/8 ha\). Dit betekent dat de effectief op te volgen oppervlakte gelijk is aan \(9 \times 1/8 = 1.125 ha\) en het effectief aantal op te volgen locaties is \(9\).
  5. De 9 locaties van \(1/8 ha\) binnen de beheereenheid zijn bij voorkeur vierkanten (bedekkingen inschatten is iets gemakkkelijker in een vierkant), een proefvlakcirkel is echter ook mogelijk.

voorbeeld 2: er zijn 20 beheereenheden van 1 ha met natuurstreefbeeld 6510_hu. De beheereenheden liggen verspreid over een gebied van 150 ha.

  1. De totale oppervlakte is 20 ha, dus \(n = 15\) (zie Figuur C.2)
  2. Er is geen informatie over beheervragen, dus selecteren we beheereenheden zodat ze ruimtelijk een goede weerspiegeling zijn van de ligging van de 20 beheereenheden in het gebied.
  3. Elke beheereenheid die we selecteren telt als 1 teleenheid.
  4. Er moeten dus 15 beheereenheden bekeken worden om de vooropgestelde \(n\) te halen.
  5. De effectief opgevolgde oppervlakte is in dit geval 15 ha. Het effectief aantal opgevolgde locaties is eveneens 15.

voorbeeld 3: er zijn 13 beheereenheden, waarvan 9 met een oppervlakte van 5 ha en 4 met een oppervlakte van 1,5 ha en het natuurstreefbeeld is 4030.

  1. De totale oppervlakte is \(9 \times 5 + 4 \times 1,5= 51 ha\), dus \(n = 26\).
  2. Er is geen informatie over beheervragen, dus selecteren we beheereenheden zodat ze ruimtelijk een goede weerspiegeling zijn van de ligging van de beheereenheden in het gebied.
  3. Voor de 9 beheereenheden van 5 ha geldt dat ze groter zijn de maximale oppervlakte die in één keer kan opgenomen worden. Daarom worden 23 (\(26 * (9\times5/51)\), dus proportioneel met de oppervlakte) locaties gekozen en verspreid over de 9 beheereenheden.
  4. Deze 9 beheereenheden zijn groter dan de maximale oppervlakte die in één keer mag beoordeeld worden. We corrigeren de aanbevolen oppervlakte naar beneden (zie Tabel C.2). In een beheereenheid zullen gemiddeld \(23/9 = 2.6\) locaties beoordeeld worden. In geval van 1 of 2 herhalingen in een beheereenheid zal een proefvlak \(1 ha\) zijn, in geval van 3 (tot max. 7) herhalingen \(1/2 ha\). Indien we veronderstellen dat in 7 beheereenheden 3 proefvlakken bekeken worden en de andere beheereenheid 2 proefvlakken, dan bekijken we \(7 \times 3 \times 1/2 + 2 = 12,5ha\) van de \(45ha\).
  5. Voor de overige 3 locaties kiest men 3 van de 4 percelen met een oppervlakte van 1,5 ha die men volledig opvolgt.

voorbeeld 4: Er zijn twee plassen met als natuurstreefbeeld 3140. De ene plas heeft een omtrek van 1500m (15 ha), de andere heeft een omtrek van 300m (0.5 ha). Beide plassen zijn in goede staat, maar de grote plas ondervindt mogelijk negatieve invloed van een milieudruk afkomstig uit zuidelijke richting.

  1. In totaal is er 1800 m oeverlengte en 15.5 ha, dus \(n = 12\) of omgezet naar oeverlengte (veronderstel een cirkelvorm) is dit \(1396m\).
  2. Omwille van de milieudruk wordt besloten enkel de grote plas op te volgen.
  3. De totale omtrek van de plas is groter dan het maximum voor het type. Er worden \(r = 12\) transecten verdeeld over de oever van de plas.
  4. De transectlengte wordt naar beneden gecorrigeerd: \(a_{aanb} / \sqrt{r} = 100 / \sqrt{12} \approx 30 m\). In totaal wordt \(12 \times 30 = 360m\) oeverlengte opgevolgd op 12 oeversegmenten.

  1. We kunnen geen optimale steekproefgrootte opgeven omdat dit van de variabiliteit in elk gebied en van de (beheer)vragen afhangt. Stel bijvoorbeeld dat een indicator een gemiddelde bedekking van 50% met standaarddeviatie van 25% heeft in het gebied. Dan geeft dit met \(n = 50\) een 95% betrouwbaarheidsinterval van \(\pm 7\%\) rond het geschat gemiddelde. We moeten er echter rekening mee houden dat omwille van waarnemereffecten en het ordinale karakter van de bedekkingsschaal er een bijkomend informatieverlies is waardoor de onzekerheid op de schatting groter zal zijn. Stel nu dat we een verschil tussen twee beheervormen willen opvolgen. Met een totale steekproefgrootte van \(n = 50\) hebben we dan \(25\) herhalingen in elke groep. In dat geval kunnen we met 80% onderscheidend vermogen een verschil gelijk aan \(0/8 \times\) de standaarddeviatie aantonen tussen de groepen indien we veronderstellen dat beide groepen een normale verdeling volgen met dezelfde standaarddeviatie. Merk echter op dat in de praktijk van beheeropvolging een beheerder beslissing moet nemen op basis van \(n = 1\) (weliswaar meerdere indicatoren + terreinkennis + ervaring), aangezien de meeste beheervragen zich toespitsen op één beheereenheid.↩