3 Statische verwerking
3.1 Basismodel
We beschouwen een eenvoudig statistisch model om het aantal koppels per telblok te beschrijven. We veronderstellen dat het aantal koppels afhangt van drie factoren:
- De oppervlakte van het telblok. Het aantal koppels is rechtevenredig met de oppervlakte open ruimte binnen het telblok.
- De gemiddelde dichtheid van patrijs.
- De WBE. Het landschap kan sterk verschillen tussen de WBE’s. Het ene landschap is geschikter voor patrijs dan het andere landschap. We kunnen redelijkerwijs veronderstellen dat de dichtheid in de ene WBE verschilt van een andere WBE.
- Wie de monitoring uitvoert: de lokale jager of de externe partij.
Deze laatste factor is het doel van deze analyse. We willen nagaan of er al dan niet een verschil is tussen tellingen uitgevoerd door lokale jagers of door de externe partij. En als er een verschil is, hoe groot is het en in welke richting.
Hieronder geven we de wiskundige voorstelling van het model. Het aantal koppels \(Y_t\) in telblok \(t\) volgt een Poisson verdeling met gemiddelde \(\lambda_t\) (3.1). Het gemiddelde \(\lambda_t\) koppelen met we met een log-link naar de lineaire predictor \(\eta_t\) (3.2). Deze lineaire predictor \(\eta_t\) hangt af van de log oppervlakte van het telblok \(\beta_a \log O_t\) in km² (1 km² = 100 ha), de gemiddelde globale dichtheid \(\beta_0\), het verschil in gemiddelde dichtheid \(b_w\) in de WBE \(w\) t.o.v. het globale gemiddelde en wie de telling uitvoerde \(\beta_m X\) (3.3). Het WBE-effect \(b_w\) modelleren we als een random intercept met gemiddelde 0 en variantie \(\sigma_w^2\) (3.4).
\[\begin{align} Y_t &\sim \mathcal{P}(\lambda_t) \tag{3.1}\\ \log\lambda_t &= \eta_t \tag{3.2}\\ \eta_t &= \beta_a \log O_t + \beta_0 + b_w + \beta_m X \tag{3.3}\\ b_w &\sim \mathcal{N}(0, \sigma^2_w) \tag{3.4} \end{align}\]
We schatten de parameters van dit model in een Bayesiaans framework met behulp van Integregated Nested Laplacing Approximation (INLA). Hiervoor dienen we een aantal priors in te stellen. We kiezen de prior voor \(\beta_a\) bewust zeer informatieve zodat in de praktijk \(\beta_a = 1\).
- \(\beta_a \sim \mathcal{N}(1, 10^{-6})\)
- \(\beta_0 \sim \mathcal{N}(0, 100)\)
- \(\beta_m \sim \mathcal{N}(0, 100)\)
- \(P(\sigma_w > 0.4) = 0.05\)
Wanneer de lokale jagers het telblok monitoren stellen we \(X = 0\). In het geval de externe partij de monitoring uitvoert stellen we \(X = 1\). Voor een gemiddelde WBE volgt uit (3.4) dat \(b_w = 0\). De lineaire predictor voor een telblok van 1 km² in een gemiddelde WBE, onderzocht door de lokale jagers, vereenvoudigt tot \(\eta_0 = \beta_0\). De lineaire predictor voor een telblok van 1 km² in een gemiddelde WBE, onderzocht door de externe partij, vereenvoudigt tot \(\eta_1 = \beta_0 + \beta_m\). M.a.w. \(\beta_m\) is het verschil in lineaire predictor dat we kunnen verklaren door wie het telblok onderzocht. Aangezien we een log-link gebruiken (3.2), moeten we het terugtransformeren.
De maat waarin we geïnteresseerd zijn is bijgevolg \(\exp(\beta_m)\). Deze kunnen we interpreteren als het relatieve verschil in dichtheid in een telblok wanneer de externe partij telt i.v.m. eenzelfde telling door de lokale jagers.
Op basis van het model schatten we dit verschil als +23% (+9%; +38%). Het eerste getal is de eigenlijke schatting. De twee getallen tussen de haakjes geven het 95% geloofwaardig interval. Wanneer dit interval 0% niet bevat, kunnen we spreken van een significant effect. Voor 2021 kunnen we dus besluiten dat er een significant verschil is tussen wanneer lokale jagers of de externe partij gaat tellen. De externe partij telt hierbij ongeveer een kwart meer koppels in vergelijking met de lokale jagers.
3.2 Invloed van het aantal bezoeken
In principe monitoren we elk telblok vier keer. In de praktijk zijn een aantal telblokken minder vaak onderzocht. Hoe vaker we een telblok onderzoeken, hoe groter de kans dat we een patrijs minstens eenmaal waarnemen. In tabel 3.1 geven we het aantal telblokken met 1, 2, 3 of 4 bezoeken. Merk op dat een kwart van de telblokken minder dan de voorschreven vier keer bezocht werden. Merk op dat we in dit rapport de telblokken zonder waarnemingen van patrijs niet gebruiken. Voor deze analyse zijn ze niet relevant. Voor het bepalen van de gemiddelde dichtheid van de WBE gebruiken we ze wel.
| bezoeken | aantal telblokken |
|---|---|
| 1 | 158 |
| 2 | 207 |
| 3 | 380 |
| 4 | 2175 |
We brengen het aantal bezoeken in rekening door aan de lineaire predictor een term \(b_b\) toe te voegen (3.5). We modelleren het effect als een tweede orde toevalsbeweging (3.6). Op deze manier krijgen we een enigszins continu patroon zonder dat we expliciet de vorm van het verband a priori vastleggen. Als prior voor dit effect kiezen we \(P(\sigma_b > 0.01) = 0.05\).
\[\begin{align} Y_t &\sim \mathcal{P}(\lambda_t)\\ \log\lambda_t &= \eta_t\\ \eta_t &= \beta_a \log O_t + \beta_0 + b_w + \beta_m X + b_b \tag{3.5}\\ b_w &\sim \mathcal{N}(0, \sigma^2_w)\\ \Delta^2b_b &\sim \mathcal{N}(0, \sigma^2_b)\tag{3.6} \end{align}\]
Figuur 3.1 heeft aan dat het aantal bezoeken duidelijk een invloed heeft op het aantal waargenomen koppels. Door de schuwe levenswijze van de patrijs volstaat één bezoek duidelijk niet. Na drie bezoeken vinden ca 80% van het aantal koppels dat we vinden na 4 bezoeken. We kunnen stellen dat we minstens vier bezoeken nodig hebben.
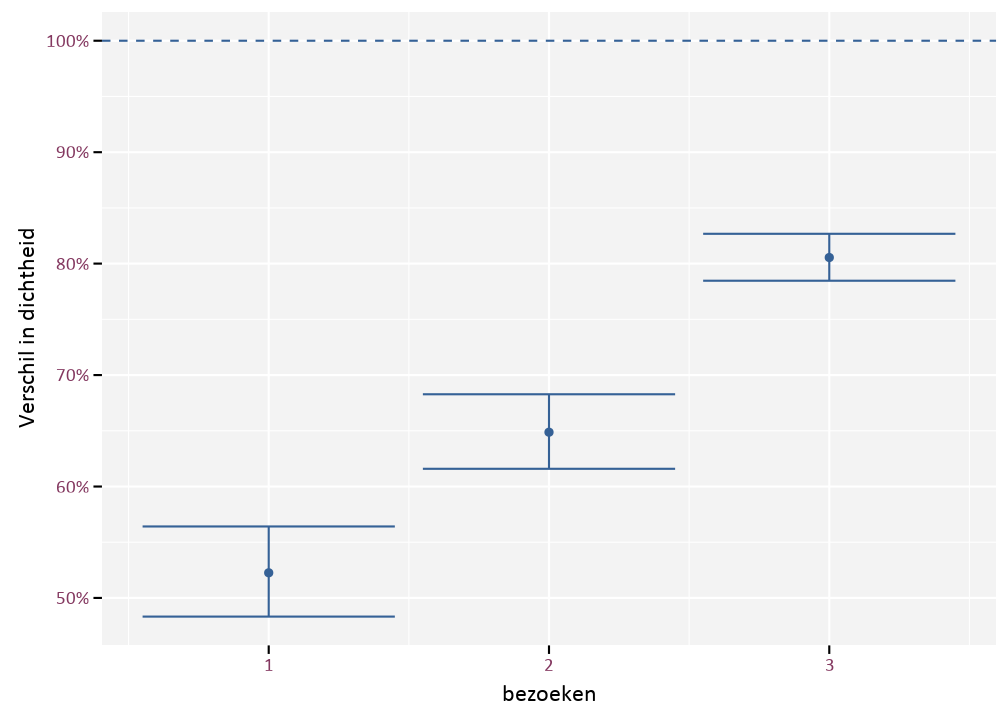
Figuur 3.1: Waargenomen relatief verschil in dichtheid t.o.v. 4 bezoeken.
Wanneer we het aantal bezoeken in rekening brengen, is het verschil tussen de externe partij en de lokale jagers +22% (+8%; +36%). Dat is nagenoeg identiek aan het oorspronkelijke model: +23% (+9%; +38%). Omdat slechts weinig telblokken extreem weinig bezocht werden, is de invloed van het aantal bezoeken beperkt op het geschatte verschil tussen de externe partij en de lokale jagers.
3.3 Anomalieën
Het bovenstaande model onderzocht het verschil tussen tellingen uitgevoerd door lokale jagers en deze uitgevoerd door een externe partij op het niveau van de deelnemende WBE’s. De gegevens laten echter ook toe om afwijkende telgegevens op het niveau van een telblok te identificeren. Hiervoor kijken we naar de Pearson afwijkingen van de waarnemingen. Deze vergelijken de waargenomen aantallen met de voorspelde aantallen volgens het model. Hoe groter de absolute waarde van de afwijking, hoe sterker het verschil tussen de waarneming en het model. Het loont de moeite om de meeste extreme afwijkingen als mogelijke anomaliën te beschouwen. Ze zijn het gevolg van ofwel het model dat sterk afwijkt van de realiteit ofwel van waarnemingen die sterk afwijken van het globale patroon. Bijvoorbeeld telblokken met beduidend hogere of lagere dichtheid in vergelijking met de overige telblokken van dezelfde WBE. We stellen vast dat verschillende telblokken een Pearson afwijking hebben die behoorlijk sterk is (fig. 3.2). Het loont de moeite om de waarnemingen van deze telblokken nader te inspecteren om na te gaan wat er aan de hand is. In tabel 3.2 lijsten we de telblokken op met de 30 meest extreme Pearson afwijkingen. We stellen vast dat in deze telblokken de waarnemingen aanleiding geven tot dichtheden die 3 tot 6 keer hoger zijn dan dat we volgens het model verwachten voor die WBE, die oppervlakte van het telblok en dat aantal bezoeken. Hierbij merken we op dat we dergelijke afwijkingen t.o.v. het model enkel in de positieve richting vaststellen en niet in de negatieve richting. Dit laatste zou betekenen dat er extreem minder patrijzen gerapporteerd worden dan het model verwacht.
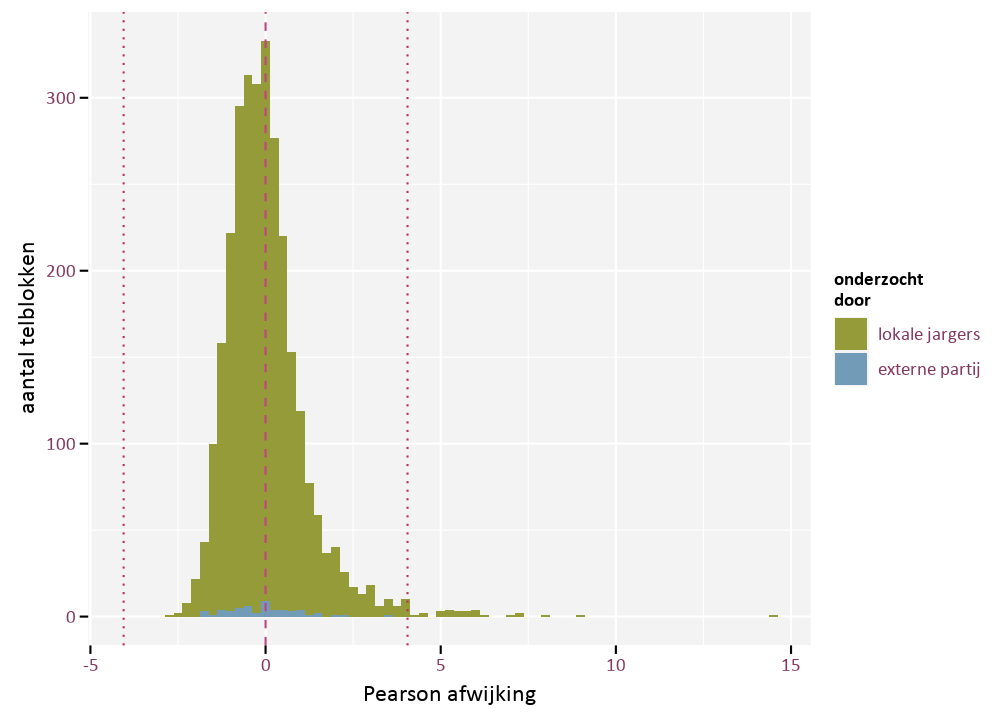
Figuur 3.2: Histogram van de Pearson afwijkingen. De 30 meest extreme afwijkingen zitten voorbij de stippellijnen.
| WBE | bezoeken | koppels | km2 | waargenomen | verwacht | verhouding |
|---|---|---|---|---|---|---|
| A | 4 | 42.7 | 1.3 | 33.9 | 5.0 | 6.7 |
| B | 4 | 18.5 | 0.7 | 25.6 | 4.2 | 6.1 |
| C | 2 | 19.6 | 0.7 | 27.6 | 5.5 | 5.0 |
| D | 4 | 22.3 | 1.0 | 22.6 | 5.4 | 4.2 |
| E | 4 | 20.3 | 0.7 | 27.7 | 6.2 | 4.4 |
| A | 4 | 18.5 | 0.8 | 22.5 | 5.0 | 4.5 |
| F | 4 | 13.9 | 0.6 | 23.2 | 5.0 | 4.6 |
| B | 4 | 15.0 | 0.8 | 17.7 | 4.2 | 4.2 |
| G | 3 | 10.8 | 0.6 | 17.4 | 3.4 | 5.2 |
| E | 4 | 25.3 | 1.3 | 19.4 | 6.2 | 3.1 |
| E | 4 | 18.7 | 0.8 | 22.5 | 6.2 | 3.6 |
| A | 4 | 17.9 | 1.0 | 18.0 | 5.0 | 3.6 |
| A | 3 | 12.8 | 0.7 | 17.4 | 4.1 | 4.3 |
| H | 4 | 17.7 | 0.6 | 30.2 | 8.6 | 3.5 |
| F | 3 | 11.9 | 0.7 | 18.0 | 4.1 | 4.4 |
| I | 4 | 26.9 | 1.1 | 23.7 | 8.7 | 2.7 |
| J | 1 | 11.0 | 1.1 | 10.2 | 2.3 | 4.4 |
| K | 4 | 16.6 | 1.0 | 16.0 | 4.8 | 3.3 |
| L | 4 | 19.4 | 1.1 | 17.9 | 5.9 | 3.1 |
| M | 4 | 20.5 | 1.2 | 17.7 | 6.0 | 3.0 |
| F | 4 | 20.5 | 1.4 | 14.9 | 5.0 | 2.9 |
| G | 2 | 13.0 | 1.3 | 10.1 | 2.7 | 3.7 |
| N | 3 | 14.5 | 0.6 | 22.5 | 6.4 | 3.5 |
| O | 2 | 14.1 | 0.9 | 15.1 | 4.4 | 3.4 |
| K | 4 | 18.3 | 1.4 | 13.4 | 4.8 | 2.8 |
| P | 4 | 12.8 | 0.7 | 18.0 | 5.6 | 3.2 |
| Q | 4 | 17.0 | 1.4 | 12.4 | 4.6 | 2.7 |
| R | 1 | 10.0 | 0.9 | 10.7 | 3.2 | 3.4 |
| S | 3 | 10.0 | 0.6 | 18.0 | 5.3 | 3.4 |
| F | 4 | 12.1 | 0.8 | 15.3 | 5.0 | 3.0 |

