5 Opdelen van open ruimte in telblokken
De wildbeheereenheden die wensen te jagen op patrijs, dienen de patrijzen te monitoren binnen de open ruimte in hun werkingsgebied. Volgens Agentschap voor Natuur en Bos (2021) kan een teller een gebied van 125 tot 175 ha inventariseren. Daarom delen we de open ruimte van de WBE op in een meerdere telblokken. Hierbij streven we naar telblokken die hoogstens 150 ha open ruimte bevatten. Vanuit de jagerij kwam het signaal dat ze verkiezen om geen telblokken te hebben die meerdere jachtterreinen omvatten. Aangezien sommige jachtterreinen weinig open ruimte bevatten zullen sommige telblokken hierdoor klein zijn. Het is de bedoeling dat we van elk telblok een kaart maken die afdrukbaar is op een A4 bij schaal 1:10.000. Daarom moet elk telblok passen binnen een begrenzingsvak met een lange zijde van maximum 2500 m en korte zijde van maximum 1900 m.
In een eerste stap gaan we na voor welke jachtterreinen de open ruimte kleiner dan 150 ha is en het geheel een begrenzingsvlak heeft dat voldoende klein is. Voor deze jachtterrein is de volledige open ruimte binnen het jachtterrein het telblok.
Bij de grotere jachtterreinen zullen we eerste de open ruimte in kleinere eenheden splitsen. Eerst relatief kleine eenheden maken en die nadien samenvoegen tot telblokken, laat toe een zo goed mogelijke indeling te maken. Daarom streven we in deze fase naar eenheden kleiner dan 50 ha en met een begrenzingsvak van minder dan 1900 m langs elke zijde. In eerste instantie kijken we naar de reeds bestaande eenheden binnen een jachtterrein. Deze eenheden zijn volledig van elkaar gescheiden door delen die geen open ruimte of geen jachtgebied zijn. Eenheden die reeds voldoende klein zijn (< 150 ha en begrenzingsvak < 1900 m langs elke zijde) zetten we apart.
Grotere eenheden proberen we in kleinere eenheden te splitsen langs grenzen die in het veld duidelijk zichtbaar zijn.
Hiervoor gebruiken we de beschikbare informatie over wegen (highway) en waterlopen (waterway) uit OpenStreetMap.
Tabel 5.1 toont welke elementen we gebruiken en in welke volgorde.
We starten met de belangrijkste elementen die er toe doen.
Vandaar dat we eerst splitsen langs steenwegen en dan langs lokale verbindingswegen.
Splitsen langs belangrijkere wegen zoals snelwegen is niet relevant aangezien er geen eenheden zijn waar een snelweg doorloopt.
Na elke split zetten we de eenheden die nu voldoende klein zijn apart.
De overige eenheden splitsen we met het volgende element.
Wanneer we alle elementen van tabel 5.1 afgewerkt hebben blijven er nog een paar grote eenheden over.
Mogelijk zijn in deze gebieden nog niet alle elementen toegevoegd aan OpenStreetMap.
Een andere mogelijkheid is dat er in het gebied geen elementen aanwezig zijn die de eenheid doorsnijden.
We kunnen niet anders dan deze eenheden als telblokken groter dan 150 ha te gebruiken.
| key | value | omschrijving |
|---|---|---|
| highway | secondary | steenwegen |
| highway | tertiary | lokale verbindingswegen |
| waterway | stream | beek |
| highway | unclassified | lokale wegen |
| highway | track | veldweg geschikt voor landbouwvoertuigen |
| waterway | ditch | gracht |
| waterway | ditch | afwateringskanaal |
| highway | path | veldweg niet geschikt voor landbouwvoertuigen |
| highway | service | private toegangsweg |
Nu we de open ruimte in kleinere eenheden opgedeeld hebben, komen we in de fase dat we deze eenheden terug samenvoegen tot telblokken. We kijken per jachtterrein welke eenheden vlak bij elkaar liggen. In figuur 5.1 geven we een fictief voorbeeld van een aantal eenheden in een jachtgebied.
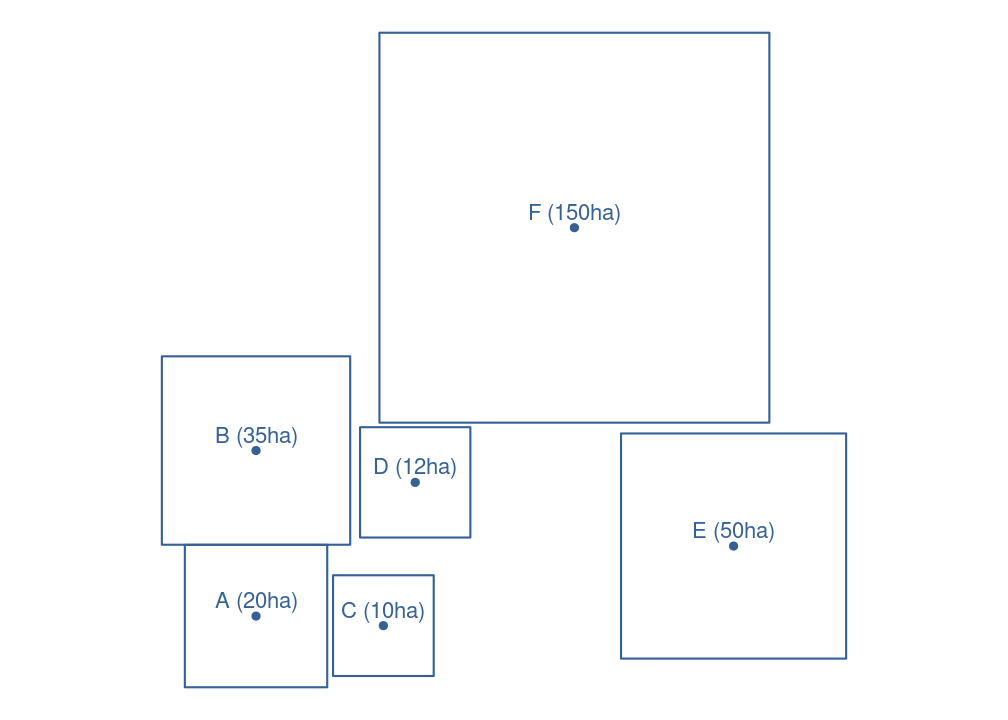
Figuur 5.1: Voorbeeld met een aantal fictieve eenheden met aanduiding van hun zwaartepunt, label en oppervlakte.
Om dit te kunnen automatiseren bepalen we eerst van elke eenheid zijn zwaartepunt (zwaartepunt).
Vervolgens berekenen we een Delaunay-triangulatie van deze zwaartepunten.
Op deze manier verbinden we twee zwaartepunten zodat een set van niet overlappende driehoeken ontstaat.
We veronderstellen dat, wanneer het zwaartepunt van twee eenheden met elkaar verbonden is, deze eenheden naast elkaar liggen zonder dat er een andere eenheid tussen ligt.
Wanneer deze eenheden gescheiden zijn door iets wat geen open ruimte is (bos, dorpskern, …) kan het zijn dat ze alsnog ver uit elkaar liggen.
Daarom beperken we ons tot de verbonden zwaartepunten die minder dan 1 km uit elkaar liggen.
In figuur 5.2 tonen we de Delaunay-triangulatie toegepast op het voorbeeld uit fig. 5.1.
Merk op dat eenheid E te ver van de andere eenheden ligt.
We verbreken ook verbindingen met eenheden die reeds te groot zijn.
In het voorbeeld is dat F.
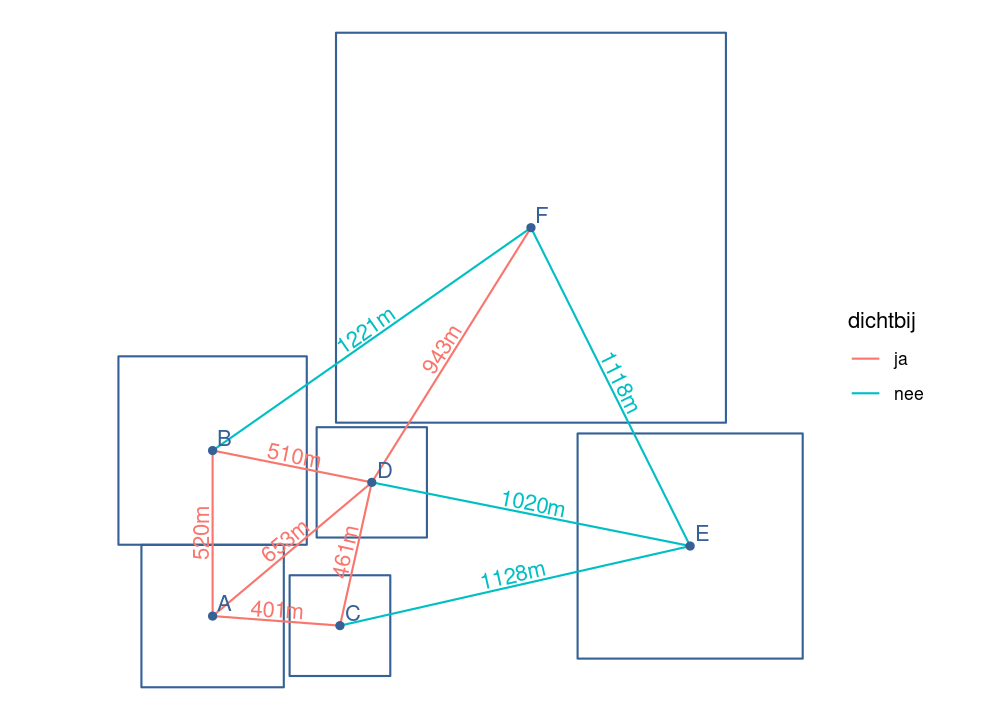
Figuur 5.2: Toevoegen van Delaunay-triangulatie met aanduiding van de afstand tussen de zwaartepunten.
We willen zoveel mogelijk kleine telblokken vermijden.
Dat kunnen we door te kijken bij welke eenheden we de kleinste eenheid kunnen samenvoegen.
We kijken met welke eenheden de kleinste eenheid verbonden is.
In ons voorbeeld is C de kleinste eenheid en deze is verbonden met A en D.
De vraag is nu welke groep het meest compacte resultaat geeft.
We vatten de compactheid van een groep van \(N\) eenheden in formule (5.1).
Hierbij is \(O_i\) de oppervlakte van de eenheid \(i\) in ha, \(L_i\) de langste zijde en \(K_i\) de kortste zijde van het begrenzingsvak.
Hoe kleiner de waarde van \(O_i\), \(L_i\) en \(K_i\), hoe compacter het telblok \(i\) is.
De globale maat \(P\) hangt enerzijds af van het aantal telblokken en anderzijds van hun compactheid.
Een lage \(P\) is een goede balans tussen zo weinig mogelijk telblokken en compacte telblokken.
In tabel 5.2 geven we deze maten voor elke eenheid of groep van eenheden.
(Groepen van) eenheden die niet voldoen aan de voorwaarden \(O_i < 150\), \(L_i < 2500\) en \(K_i < 1900\) zijn te groot en gebruiken we niet.
\[\begin{equation} P = \sum^N_{i=1} \left(\frac{O_i}{150} + \frac{L_i}{2500} + \frac{K_i}{1900}\right) \tag{5.1} \end{equation}\]
| groep | \(O_i\) | \(L_i\) | \(K_i\) | \(P_i\) |
|---|---|---|---|---|
| C | 10 | 316 | 316 | 0.36 |
| D | 12 | 346 | 346 | 0.40 |
| A | 20 | 447 | 447 | 0.55 |
| CD | 22 | 316 | 316 | 0.44 |
| AC | 30 | 447 | 352 | 0.56 |
| B | 35 | 592 | 592 | 0.78 |
| ACD | 42 | 447 | 352 | 0.64 |
| BD | 47 | 592 | 369 | 0.74 |
| E | 50 | 707 | 707 | 0.99 |
| ABCD | 77 | 519 | 352 | 0.91 |
| combinatie | P |
|---|---|
| A, B, C, D, E | 3.08 |
| A, B, CD, E | 2.76 |
| AC, B, D, E | 2.73 |
| ACD, B, E | 2.41 |
| AC, BD, E | 2.30 |
| ACBD, E | 1.89 |
In tabel 5.3 geven we de totale compactheidscore voor verschillende combinaties van (groepen van) eenheden.
We zien dat C samenvoegen met A of D een betere (lagere) score geeft.
De beste combinatie is deze waarbij we A en C samenvoegen.
De kleinste eenheid is nu D, welke verbonden is met AC en B.
De beste combinatie daarvan is BD.
Wat er voor zorgt dat AC de kleinste eenheid is, welke alleen met BD verbonden is.
Nadat we deze samenvoegen tot ABCD, is E de kleinste eenheid.
Deze heeft geen verbindingen met andere eenheden, zodat we deze overslaan.
De tweede kleinste eenheid is ABCD welke eveneens geen verbindingen heeft en we bijgevolg overslaan.
Nu hebben we alle eenheden behandeld en krijgt dit fictieve jachtterrein drie telblokken ABCD, E en F.
Referenties

