Skip to contents

Model data with missing observations using multiple imputation

Thierry Onkelinx

2018-01-12

Source: vignettes/impute.Rmd
impute.Rmd

The multimput package

The multimput package was originally intended to provide the data and code to replicate the results of Onkelinx, Devos, and Quataert (2016). This paper is freely available at http://dx.doi.org/10.1007/s10336-016-1404-9. The functions were all rewritten to make them more user-friendly and more generic. In order to make the package more compact, we removed the original code and data starting for version 0.2.6. However both the original code and data remain available in the older releases.

Very short intro to multiple imputation

  1. Create the imputation model
  2. Generate imputations for the missing observation
  3. Aggregate the imputed data
  4. Model the aggregated imputed data

Short intro to multiple imputation

The imputations are based on a model Y∼Xβ*Y \sim X \beta^* which the user has to specify. For a missing value ii with covariates xix_i, we draw a random value yiy_i from the distribution of ŷi\hat{y}_i. In case of a linear model, we sample a normal distribution yi∼N(ŷi,σi)y_i \sim N(\hat{y}_i, \sigma_i). An imputation set ll holds an impute value yiy_i for each missing value.

With the missing values replaced by imputation set ll, the dataset is complete. So we can apply the analysis that we wanted to do in the first place. This can, but don’t has to, include aggregating the dataset prior to analysis. The analysis results in a set of coefficients γal{\gamma_a}_l and their standard error σal{\sigma_a}_l. Of course, this set will depend on the imputed values of the imputation set ll. Another imputation set has different imputed values and will hence lead to different coefficients.

Therefore the imputation, aggregation and analysis is repeated for LL different imputation sets, resulting in LL sets of coefficients and their standard errors. They are aggregated by the formulas below. The coefficient will be the average of the coefficient in all imputation sets. The standard error of a coefficient is the square root of a sum of two parts. The first part is the average of the squared standard error in all imputation sets. The second part is the variance of the coefficient among the imputation sets, multiplied by a correction factor 1+1L1 + \frac{1}{L}.

γ‾a=∑l=1LγalL\bar{\gamma}_a = \frac{\sum_{l = 1}^L{\gamma_a}_l}{L}

σ‾a=∑l=1Jσa2lL+(1+1L)∑l=1L(γal−γ‾a)2L−1\bar{\sigma}_a = \sqrt{\frac{\sum_{l = 1}^J {{\sigma_a^2}_l}}{L} + (1 + \frac{1}{L}) \frac{\sum_{l = 1}^L({\gamma_a}_l - \bar{\gamma}_a) ^ 2}{L - 1}}

The dataset

First, let’s generate a dataset and set some observations missing. generateData() creates a balanced dataset with repeated visits of a number of sites. Each site is visited several years and multiple times per year. Have a look at the help-file of generateData() for more details on the model.

library(multimput)
set.seed(123)
prop_missing <- 0.5
dataset <- generate_data(n_year = 10, n_period = 6, n_site = 50, n_run = 1)
dataset$Observed <- dataset$Count
which_missing <- sample(nrow(dataset), size = nrow(dataset) * prop_missing)
dataset$Observed[which_missing] <- NA
dataset$fYear <- factor(dataset$Year)
dataset$fPeriod <- factor(dataset$Period)
dataset$fSite <- factor(dataset$Site)
str(dataset)
## 'data.frame':    3000 obs. of  10 variables:
##  $ Year    : int  1 2 3 4 5 6 7 8 9 10 ...
##  $ Period  : int  1 1 1 1 1 1 1 1 1 1 ...
##  $ Site    : int  1 1 1 1 1 1 1 1 1 1 ...
##  $ Mu      : num  11.36 9.31 11.33 10.98 9.79 ...
##  $ Run     : int  1 1 1 1 1 1 1 1 1 1 ...
##  $ Count   : num  8 2 10 21 2 2 13 8 10 4 ...
##  $ Observed: num  NA 2 10 NA 2 NA 13 NA NA NA ...
##  $ fYear   : Factor w/ 10 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 9 10 ...
##  $ fPeriod : Factor w/ 6 levels "1","2","3","4",..: 1 1 1 1 1 1 1 1 1 1 ...
##  $ fSite   : Factor w/ 50 levels "1","2","3","4",..: 1 1 1 1 1 1 1 1 1 1 ...

Variables in dataset

Year
The year of the observation as an integer
fYear
The year of the observation as a factor
Period
The period of the observation as an integer
fPeriod
The period of the observation as a factor
Site
The ID of the site as an integer
fSite
The ID of the site as a factor
Mu
The expected value of a negative binomial distribution
Count
A realisation of a negative binomial distribution with expected value Mu
Observed
The Count variable with missing data 
library(ggplot2)
ggplot(dataset, aes(x = Year, y = Mu, group = Site)) +
  geom_line() +
  facet_wrap(~Period) +
  scale_y_log10()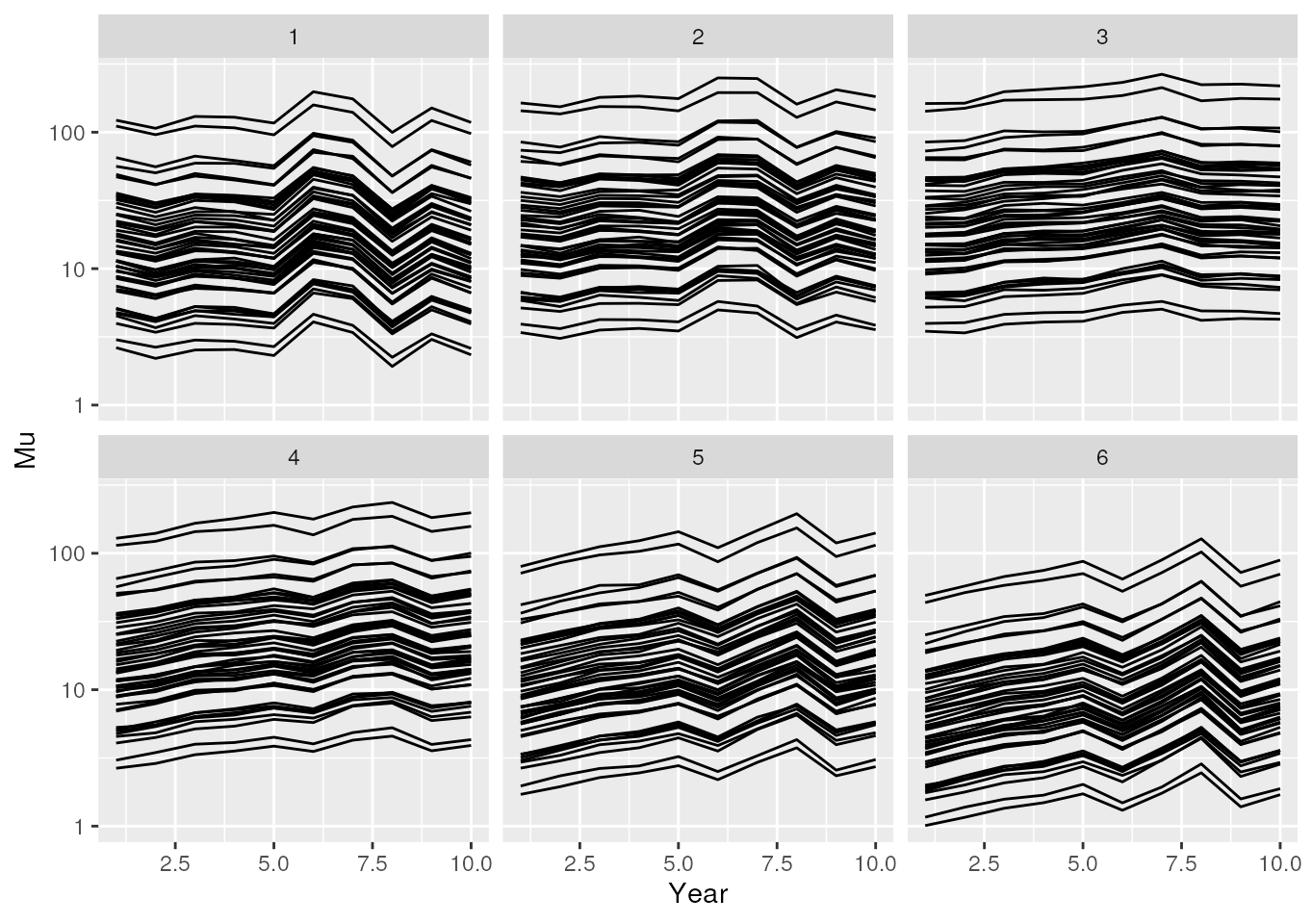
The dataset with missing observations.

The dataset with missing observations.

Create the imputation model

We will create several models, mainly to illustrate the capabilities of the multimput package. Hence several of the models are not good for a real life application.

# a simple linear model
imp_lm <- lm(Observed ~ fYear + fPeriod + fSite, data = dataset)
# a mixed model with Poisson distribution
# fYear and fPeriod are the fixed effects
# Site are independent and identically distributed random intercepts
library(lme4)
imp_glmm <- glmer(
  Observed ~ fYear + fPeriod + (1 | fSite),
  data = dataset,
  family = poisson
)
library(INLA)
# a mixed model with Poisson distribution
# fYear and fPeriod are the fixed effects
# Site are independent and identically distributed random intercepts
# the same model as imp_glmm
imp_inla_p <- inla(
  Observed ~ fYear + fPeriod + f(Site, model = "iid"),
  data = dataset,
  family = "poisson",
  control.compute = list(config = TRUE),
  control.predictor = list(compute = TRUE, link = 1)
)
# the same model as imp_inla_p but with negative binomial distribution
imp_inla_nb <- inla(
  Observed ~ fYear + fPeriod + f(fSite, model = "iid"),
  data = dataset,
  family = "nbinomial",
  control.compute = list(config = TRUE),
  control.predictor = list(compute = TRUE, link = 1)
)
# a mixed model with negative binomial distribution
# fPeriod is a fixed effect
# f(Year, model = "rw1") is a global temporal trend
#     modelled as a first order random walk
#     delta_i = Year_i - Year_{i-1} with delta_i \sim N(0, \sigma_{rw1})
# f(YearCopy, model = "ar1", replicate = Site) is a temporal trend per Site
#     modelled as an first order autoregressive model
#     Year_i_k = \rho Year_{i-1}_k + \epsilon_i_k with
#     \epsilon_i_k \sim N(0, \sigma_{ar1})
dataset$YearCopy <- dataset$Year
imp_better <- inla(
  Observed ~
    f(Year, model = "rw1") +
    f(YearCopy, model = "ar1", replicate = Site) +
    fPeriod,
  data = dataset,
  family = "nbinomial",
  control.compute = list(config = TRUE),
  control.predictor = list(compute = TRUE, link = 1)
)

Apply the imputation model

Most models have a predict method. In such a case impute() requires both a model and a data argument. Note that this implies that one can apply an imputation on any dataset as long as the dataset contains the necessary variables.

inla do the prediction simultaneously with the model fitting. Hence the model contains all required information and the data is not used.

n_imp is the number of imputations. The default is n_imp = 19.

raw_lm <- impute(imp_lm, data = dataset)
raw_glmm <- impute(imp_glmm, data = dataset)
# setting `parallel_configs = FALSE` was required to pass R CMD Check
# in practice you can use the default `parallel_configs = TRUE`
raw_inla_p <- impute(imp_inla_p, parallel_configs = FALSE)
raw_inla_nb <- impute(imp_inla_nb, parallel_configs = FALSE)
raw_better <- impute(imp_better, parallel_configs = FALSE)
raw_better_9 <- impute(imp_better, n_imp = 9, parallel_configs = FALSE)

Aggregate the imputed dataset

Suppose that we are interested in the sum of the counts over all sites for each combination of year and period. Then we must aggregate the imputations on year and period. The resulting object will only contain the imputed response and the grouping variables. The easiest way to have a variable like year both a continuous and factor is to add both Year and fYear to the grouping.

aggr_lm <- aggregate_impute(raw_lm, grouping = c("fYear", "fPeriod"), fun = sum)
aggr_glmm <- aggregate_impute(
  raw_glmm, grouping = c("fYear", "fPeriod"), fun = sum
)
aggr_inla_p <- aggregate_impute(
  raw_inla_p, grouping = c("fYear", "fPeriod"), fun = sum
)
aggr_inla_nb <- aggregate_impute(
  raw_inla_nb, grouping = c("fYear", "fPeriod"), fun = sum
)
aggr_better <- aggregate_impute(
  raw_better, grouping = c("fYear", "fPeriod"), fun = sum
)
aggr_better_9 <- aggregate_impute(
  raw_better_9, grouping = c("fYear", "fPeriod"), fun = sum
)

Model the aggregated imputed dataset

Simple example

model_impute() will apply the model_fun to each imputation set. The covariates are defined in the rhs argument. So model_fun = lm in combination with rhs = "0 + fYear + fPeriod" is equivalent to lm(ImputedResponse ~ 0 + fYear + fPeriod, data = ImputedData).

The tricky part of this function the extractor argument. This is a user defined function which must have an argument called model. The function should return a data.frame or matrix with two columns. The first column hold the estimate of a parameter of the model, the second column their standard error. Each row represents a parameter.

extractor_lm <- function(model) {
  summary(model)$coefficients[, c("Estimate", "Std. Error")]
}
model_impute(
  aggr_lm, model_fun = lm, rhs = "0 + fYear + fPeriod", extractor = extractor_lm
)
## # A tibble: 15 × 5
##    Parameter Estimate    SE   LCL   UCL
##    <fct>        <dbl> <dbl> <dbl> <dbl>
##  1 fYear1       795.   166.  469. 1121.
##  2 fYear2       858.   174.  517. 1199.
##  3 fYear3      1152.   157.  845. 1459.
##  4 fYear4      1472.   159. 1161. 1784.
##  5 fYear5       922.   159.  610. 1233.
##  6 fYear6      1539.   162. 1222. 1855.
##  7 fYear7      1508.   164. 1187. 1829.
##  8 fYear8      1262.   173.  923. 1601.
##  9 fYear9      1200.   162.  883. 1518.
## 10 fYear10     1285.   154.  982. 1587.
## 11 fPeriod2     532.   136.  266.  799.
## 12 fPeriod3     451.   149.  158.  744.
## 13 fPeriod4     555.   142.  276.  833.
## 14 fPeriod5     -72.6  142. -350.  205.
## 15 fPeriod6    -484.   141. -760. -208.

Return only the parameters associated with fYear

The extractor function requires more work from the user. This cost is compensated by the high degree of flexibility. The user doesn’t depend on the predefined extractor functions. This is illustrated by the following examples.

extractor_lm2 <- function(model) {
  cf <- summary(model)$coefficients
  cf[grepl("fYear", rownames(cf)), c("Estimate", "Std. Error")]
}
model_impute(
  aggr_lm, model_fun = lm, rhs = "0 + fYear + fPeriod",
  extractor = extractor_lm2
)
## # A tibble: 10 × 5
##    Parameter Estimate    SE   LCL   UCL
##    <fct>        <dbl> <dbl> <dbl> <dbl>
##  1 fYear1        795.  166.  469. 1121.
##  2 fYear2        858.  174.  517. 1199.
##  3 fYear3       1152.  157.  845. 1459.
##  4 fYear4       1472.  159. 1161. 1784.
##  5 fYear5        922.  159.  610. 1233.
##  6 fYear6       1539.  162. 1222. 1855.
##  7 fYear7       1508.  164. 1187. 1829.
##  8 fYear8       1262.  173.  923. 1601.
##  9 fYear9       1200.  162.  883. 1518.
## 10 fYear10      1285.  154.  982. 1587.

Predict a smoother for predefined values

Note that we pass extra arguments to the extractor function through the extractor_args argument. This has to be a list. We recommend to use a named list to avoid confusion.

library(mgcv)
new_set <- expand.grid(
  Year = pretty(dataset$Year, 20),
  fPeriod = dataset$fPeriod[1]
)
extractor_lm3 <- function(model, newdata) {
  predictions <- predict(model, newdata = newdata, se.fit = TRUE)
  cbind(predictions$fit, predictions$se.fit)
}
model_gam <- model_impute(
  aggr_lm, model_fun = gam, rhs = "s(Year) + fPeriod",
  extractor = extractor_lm3, extractor_args = list(newdata = new_set),
  mutate = list(Year = ~as.integer(levels(fYear))[fYear])
)
model_gam <- cbind(new_set, model_gam)
ggplot(model_gam, aes(x = Year, y = Estimate, ymin = LCL, ymax = UCL)) +
  geom_ribbon(alpha = 0.1) +
  geom_line()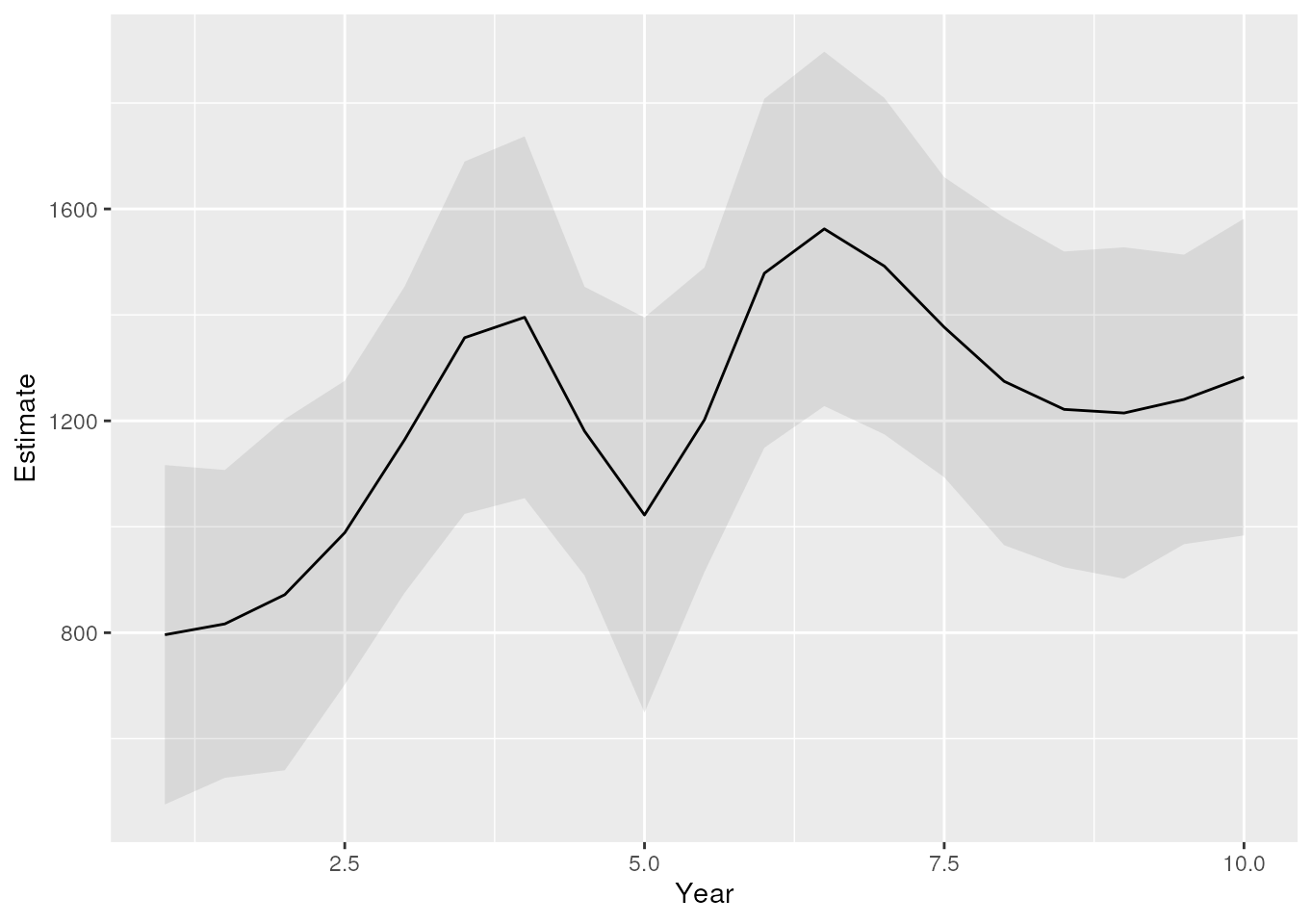
The estimated trend for the years.

The estimated trend for the years.

Compare the results using different imputation models

Modelling aggregated data with glm.nb

Suppose that we are interested in a yearly relative index taking into account the average seasonal pattern. With a complete dataset (without missing values) we could model it like the example below: a generalised linear model with negative binomial distribution because we have counts that are likely overdispersed. fYear models the yearly index and fPeriod the average seasonal pattern. The 0 + part removes the intercept for the model. This simple trick gives direct estimates for the effect of fYear.

Only the effects of fYear are needed for the index. Therefore the extractor functions selects only the parameters who’s row name contains fYear. In case that we want the first year to be used as a reference (index year 1 = 100%), we can subtract the estimate for this year from all estimates. The result are the indices relative to the first year, but still in the log scale. Note that the estimated index for year 1 will be 0 and log(100%)=0log(100\%) = 0.

library(MASS)
aggr_complete <- aggregate(
  dataset[, "Count", drop = FALSE], dataset[, c("fYear", "fPeriod")], FUN = sum
)
model_complete <- glm.nb(Count ~ 0 + fYear + fPeriod, data = aggr_complete)
summary(model_complete)
## 
## Call:
## glm.nb(formula = Count ~ 0 + fYear + fPeriod, data = aggr_complete, 
##     init.theta = 31.78765186, link = log)
## 
## Coefficients:
##          Estimate Std. Error z value Pr(>|z|)    
## fYear1    6.72514    0.09016  74.590  < 2e-16 ***
## fYear2    6.83730    0.09005  75.929  < 2e-16 ***
## fYear3    7.06993    0.08985  78.684  < 2e-16 ***
## fYear4    7.09550    0.08983  78.985  < 2e-16 ***
## fYear5    6.94750    0.08995  77.237  < 2e-16 ***
## fYear6    7.13813    0.08980  79.487  < 2e-16 ***
## fYear7    7.23272    0.08974  80.597  < 2e-16 ***
## fYear8    7.16345    0.08979  79.784  < 2e-16 ***
## fYear9    7.05221    0.08987  78.475  < 2e-16 ***
## fYear10   7.10071    0.08983  79.046  < 2e-16 ***
## fPeriod2  0.36211    0.08027   4.511 6.44e-06 ***
## fPeriod3  0.41944    0.08024   5.227 1.72e-07 ***
## fPeriod4  0.34524    0.08027   4.301 1.70e-05 ***
## fPeriod5 -0.02515    0.08045  -0.313    0.755    
## fPeriod6 -0.47112    0.08076  -5.833 5.44e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Negative Binomial(31.7877) family taken to be 1)
## 
##     Null deviance: 541101.695  on 60  degrees of freedom
## Residual deviance:     60.596  on 45  degrees of freedom
## AIC: 852.28
## 
## Number of Fisher Scoring iterations: 1
## 
## 
##               Theta:  31.79 
##           Std. Err.:  5.96 
## 
##  2 x log-likelihood:  -820.275
extractor_logindex <- function(model) {
  coef <- summary(model)$coefficients
  log_index <- coef[grepl("fYear", rownames(coef)), c("Estimate", "Std. Error")]
  log_index[, "Estimate"] <- log_index[, "Estimate"] -
    log_index["fYear1", "Estimate"]
  log_index
}

Now that we have a relevant model and extractor function, we can apply them to the aggregate imputed datasets.

model_glmm <- model_impute(
  object = aggr_glmm, model_fun = glm.nb, rhs = "0 + fYear + fPeriod",
  extractor = extractor_logindex
)
model_p <- model_impute(
  object = aggr_inla_p, model_fun = glm.nb, rhs = "0 + fYear + fPeriod",
  extractor = extractor_logindex
)
model_nb <- model_impute(
  object = aggr_inla_nb, model_fun = glm.nb, rhs = "0 + fYear + fPeriod",
  extractor = extractor_logindex
)
model_better <- model_impute(
  object = aggr_better, model_fun = glm.nb, rhs = "0 + fYear + fPeriod",
  extractor = extractor_logindex
)
model_complete <- extractor_logindex(model_complete)
colnames(model_complete) <- c("Estimate", "SE")
library(dplyr)
model_complete <- model_complete |>
  as.data.frame() |>
  mutate(
    LCL = qnorm(0.025, Estimate, SE),
    UCL = qnorm(0.975, Estimate, SE),
    Parameter = paste0("fYear", sort(unique(dataset$Year)))
  )
covar <- data.frame(
  Year = sort(unique(dataset$Year))
)
# combine all results and add the Year
parameters <- rbind(
  cbind(covar, model_glmm, Model = "glmm"),
  cbind(covar, model_p, Model = "poisson"),
  cbind(covar, model_nb, Model = "negative binomial"),
  cbind(covar, model_better, Model = "better"),
  cbind(covar, model_complete, Model = "complete")
)
# convert estimate and confidence interval to the original scale
parameters[, c("Estimate", "LCL", "UCL")] <- exp(
  parameters[, c("Estimate", "LCL", "UCL")]
)
ggplot(parameters, aes(x = Year, y = Estimate, ymin = LCL, ymax = UCL)) +
  geom_hline(yintercept = 1, linetype = 3) +
  geom_ribbon(alpha = 0.2) +
  geom_line() +
  facet_wrap(~Model)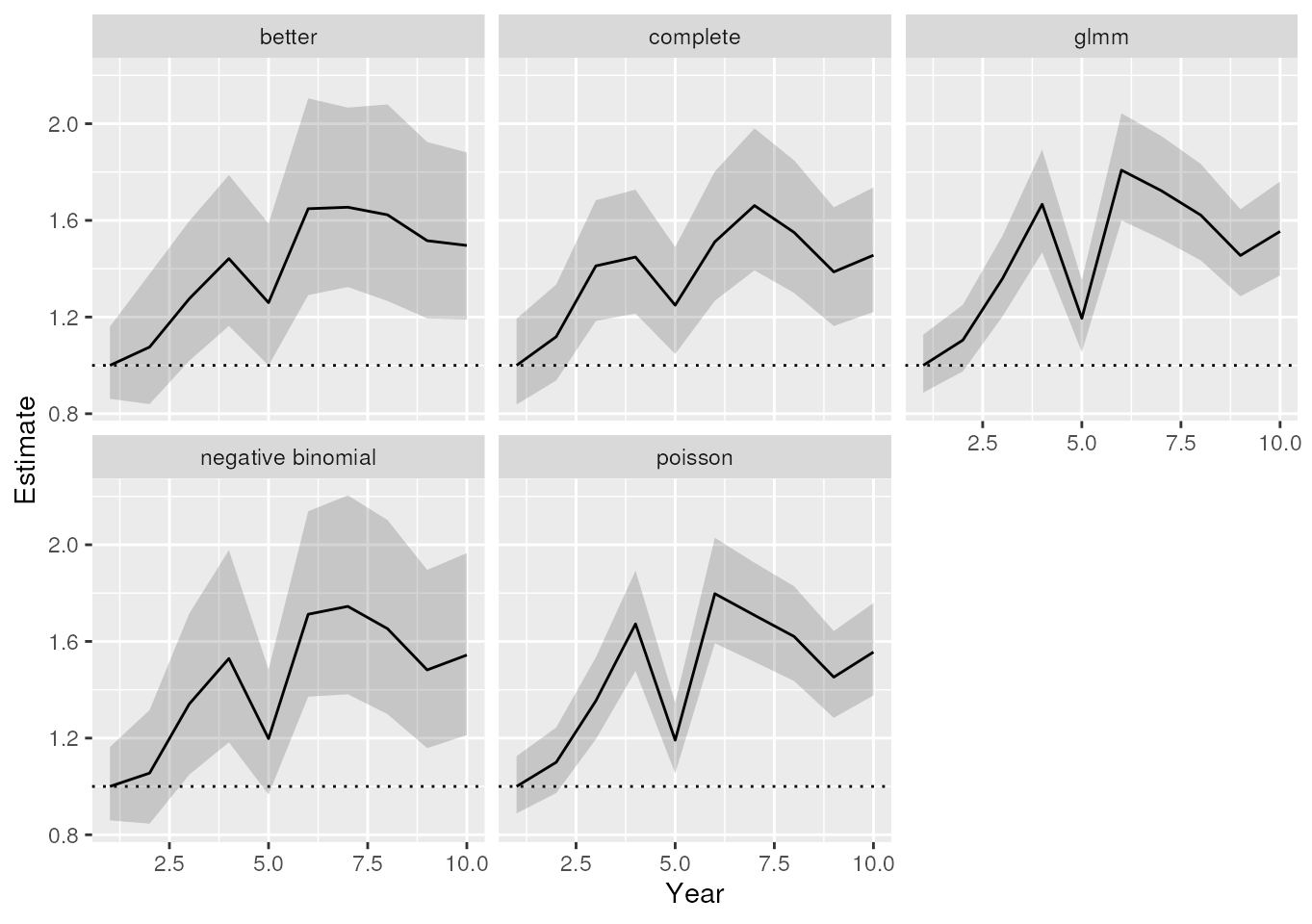
The estimated relative index for the years.

The estimated relative index for the years.

Modelling aggregated data with inla

The example below does something similar. Two things are different: 1) instead of glm.nb we use inla to model the imputed totals. 2) we model the seasonal pattern as a random intercept instead of a fixed effect.

extractor_inla <- function(model) {
  fe <- model$summary.fixed[, c("mean", "sd")]
  log_index <- fe[grepl("fYear", rownames(fe)), ]
  log_index[, "mean"] <- log_index[, "mean"] - log_index["fYear1", "mean"]
  log_index
}
model_p <- model_impute(
  object = aggr_glmm, model_fun = inla,
  rhs = "0 + fYear + f(fPeriod, model = 'iid')",
  model_args = list(family = "nbinomial"), extractor = extractor_inla
)
model_nb <- model_impute(
  object = aggr_inla_nb, model_fun = inla,
  rhs = "0 + fYear + f(fPeriod, model = 'iid')",
  model_args = list(family = "nbinomial"), extractor = extractor_inla
)
model_better <- model_impute(
  object = aggr_better, model_fun = inla,
  rhs = "0 + fYear + f(fPeriod, model = 'iid')",
  model_args = list(family = "nbinomial"), extractor = extractor_inla
)
m_complete <- inla(
  Count ~ 0 + fYear + f(fPeriod, model = "iid"), data = aggr_complete,
  family = "nbinomial"
)
model_complete <- extractor_inla(m_complete)
colnames(model_complete) <- c("Estimate", "SE")
model_complete <- model_complete |>
  as.data.frame() |>
  mutate(
    LCL = qnorm(0.025, Estimate, SE),
    UCL = qnorm(0.975, Estimate, SE),
    Parameter = paste0("fYear", sort(unique(dataset$Year)))
  )
# combine all results and add the Year
parameters <- rbind(
  cbind(covar, model_glmm, Model = "glmm"),
  cbind(covar, model_p, Model = "poisson"),
  cbind(covar, model_nb, Model = "negative binomial"),
  cbind(covar, model_better, Model = "better"),
  cbind(covar, model_complete, Model = "complete")
)
# convert estimate and confidence interval to the original scale
parameters[, c("Estimate", "LCL", "UCL")] <- exp(
  parameters[, c("Estimate", "LCL", "UCL")]
)
ggplot(parameters, aes(x = Year, y = Estimate, ymin = LCL, ymax = UCL)) +
  geom_hline(yintercept = 1, linetype = 3) +
  geom_ribbon(alpha = 0.2) +
  geom_line() +
  facet_wrap(~Model)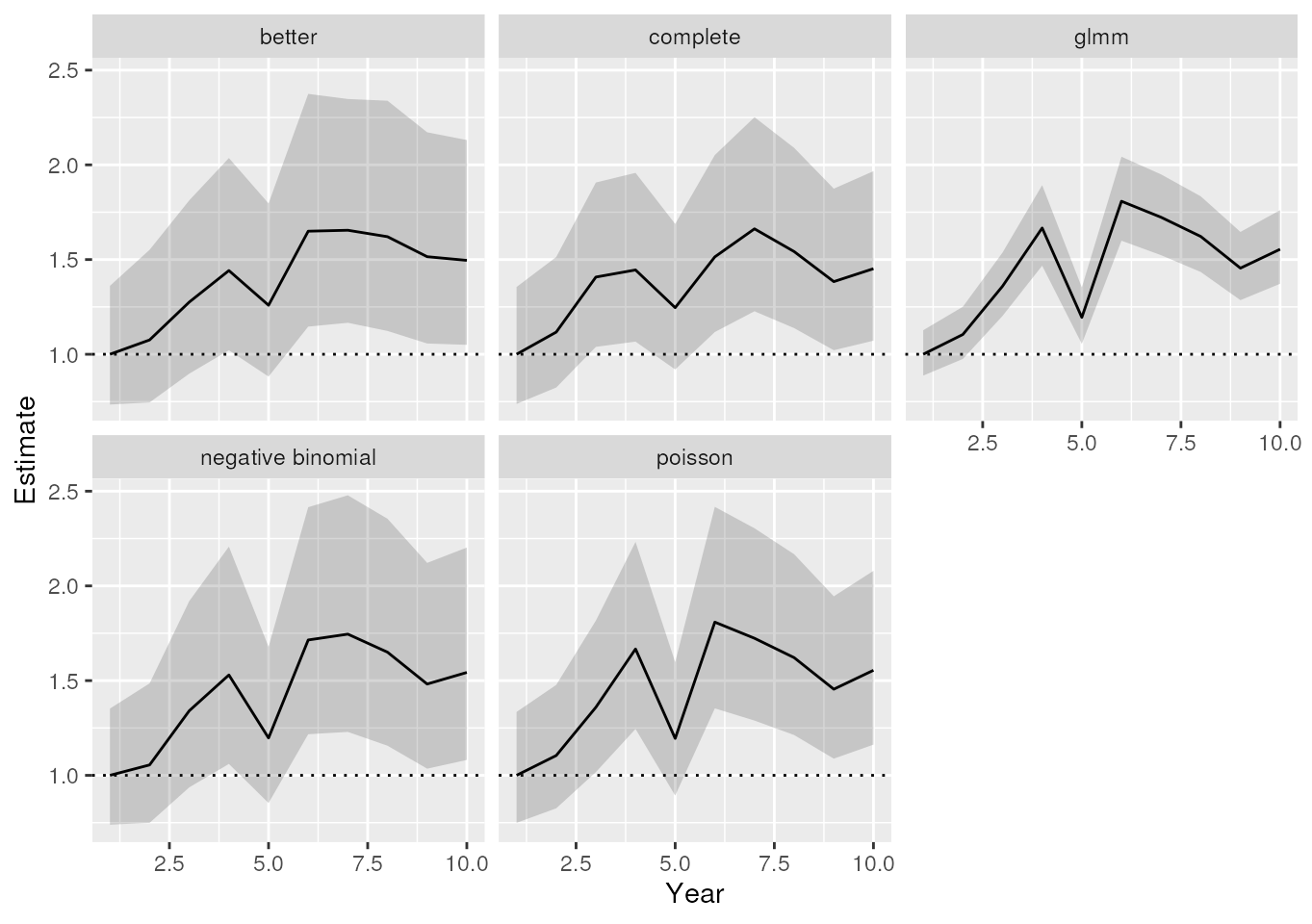
The estimated relative index for the years.

The estimated relative index for the years.

References

Onkelinx, Thierry, Koen Devos, and Paul Quataert. 2016. “Working with Population Totals in the Presence of Missing Data Comparing Imputation Methods in Terms of Bias and Precision.” Journal of Ornithology, 1–13. https://doi.org/10.1007/s10336-016-1404-9.