5 Gegevensanalyse
De manier waarop de gegevens van de soortenmeetnetten geanalyseerd worden kan sterk variëren afhankelijk van het gebruikte veldprotocol. Het veldprotocol bepaalt immers het type dataset dat bekomen wordt. We zullen dus moeten gebruik maken van verschillende analysemodellen voor de gegevensanalyse. De manier waarop we de resultaten presenteren van de analyse willen we echter zoveel mogelijk uniformiseren. We illustreren dit aan de hand van de analyseresultaten van enkele libellenmeetnetten die via het veldprotocol ‘gebiedstelling’ geteld worden. We geven eerst een korte beschrijving van het analysemodel dat hiervoor gebruikt wordt.
5.1 Beschrijving analyse gebiedstelling libellen
We geven een korte beschrijving van de twee modellen die we gebruiken voor de gegevensanalyse van de gebiedstellingen van libellen. Voor de technische achtergrond verwijzen we naar Bijlage C.
5.1.1 Model voor verschillen tussen de jaren
Via dit model modelleren we de getelde aantallen als functie van het jaar, het dagnummer en het kwadraat van het dagnummer. We gebruiken jaar als categorische variabele, zodat we een schatting per jaar krijgen. Op basis van de tweedegraads polynoom van het dagnummer modelleren we het seizoenseffect op de getelde aantallen. Ten slotte voegen we een locatie-effect toe aan het model onder de vorm van een random intercept. Hiermee geven we aan dat tellingen op eenzelfde locatie gecorreleerd zijn.
In Figuur 5.1 visualiseren we het model voor de Gevlekte witsnuitlibel. De punten geven de geobserveerde waarden weer, de zwarte lijn toont het gemiddelde seizoenseffect, de gearceerde oppervlakte komt overeen met het 95% betrouwbaarheidsinterval op het gemiddelde seizoenseffect en de stippellijnen geven de effecten per locatie weer.
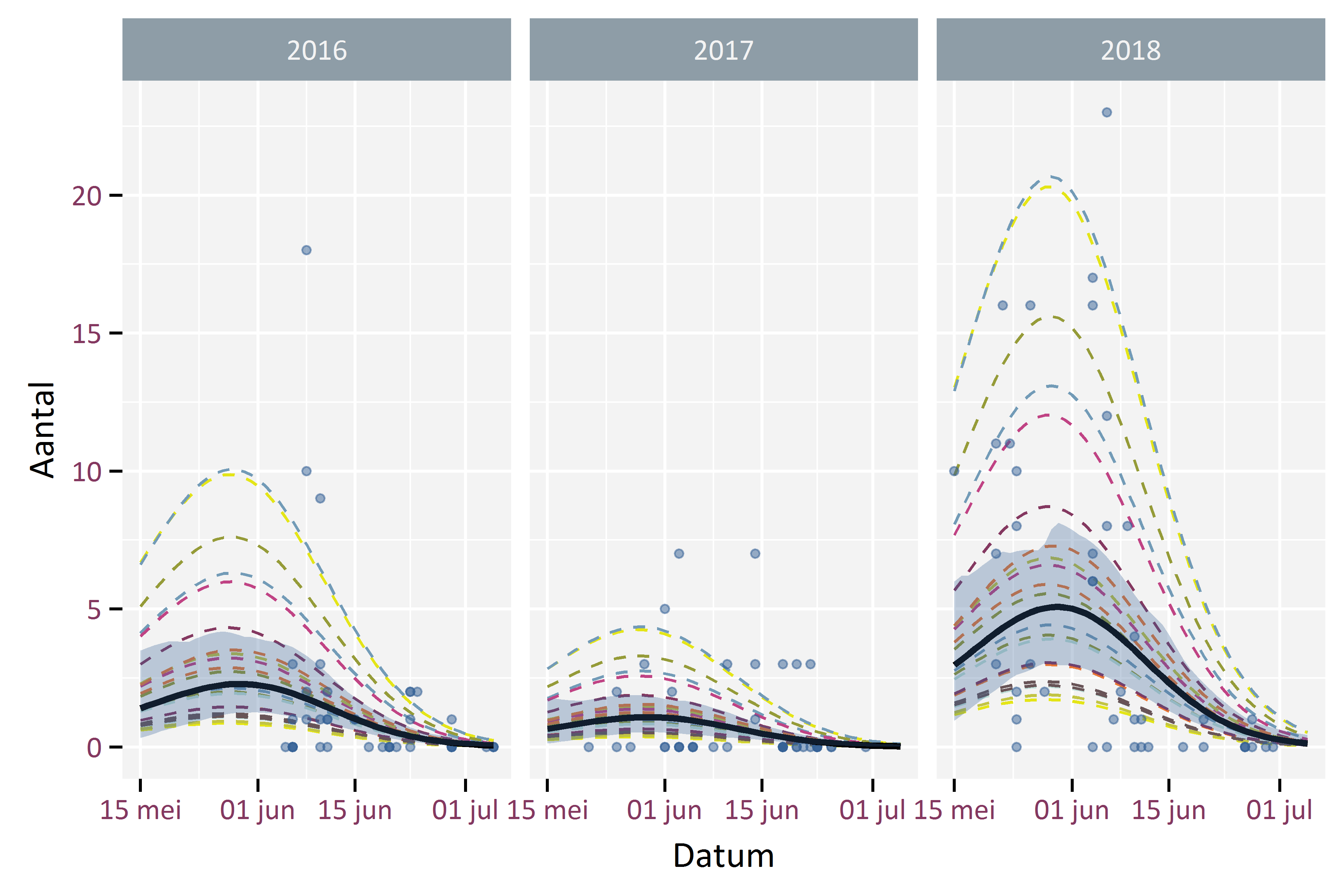
Figuur 5.1: Visualisatie analysemodel voor Gevlekte witsnuitlibel
Op basis van dit model maken we een schatting van:
de jaarlijkse index: het verschil tussen een bepaald jaar en een referentiejaar;
de gemiddelde maximale telling binnen het telseizoen per jaar.
5.1.2 Model voor lineaire trend
Om de lineaire trend te schatten gebruiken we jaar als continue variabele. Voor de rest is het model identiek aan het eerder beschreven model voor verschillen tussen de jaren.
Dit model gebruiken we voor volgende schattingen:
gemiddelde jaarlijkse lineaire trend (percentage vooruitgang of achteruitgang per jaar);
totale trend over de volledige periode (percentage vooruitgang of achteruitgang over de hele periode).
5.2 Interpretatie van trends of verschillen
Bij elke schatting van een verschil of trend hoort ook een 95%-betrouwbaarheidsinterval die de onzekerheid op de schatting weergeeft. Klassiek onderscheiden we op basis van het betrouwbaarheidsinterval:
- een significante toename: ondergrens betrouwbaarheidsinterval > 0;
- een significante afname: bovengrens betrouwbaarheidsinterval < 0;
- geen significant(e) trend of verschil: betrouwbaarheidsinterval omvat 0.
Bovenstaande indeling is echter weinig informatief. Daarom stellen we een classificatiesysteem voor waarbij het betrouwbaarheidsinterval wordt vergeleken met een referentiewaarde, een onderste drempelwaarde en een bovenste drempelwaarde. Als referentiewaarde kiezen we 0 (= geen verandering). Voor de onderste drempelwaarde kiezen we een waarde die we als een sterke afname beschouwen: -25%. Op basis van de bovenste drempelwaarde onderscheiden we een sterke toename. Hiervoor kiezen de waarde +33%, wat overeenkomt met eenzelfde relatieve effect dan een afname van -25% (75/100 = 100/133). Dit classificatiesysteem resulteert in 10 klassen (Figuur 5.2). In Tabel 5.1 geven we de codes en de beschrijving die bij de verschillende klassen horen. In figuren kunnen we de verschillende klassen visualiseren met de symbolen zoals getoond in Figuur 5.2. Deze symbolen zijn onafhankelijk van de richting van de trend, m.a.w. ++ (sterke toename) en -- (sterke afname) worden met eenzelfde symbool weergegeven en aangeduid als **.
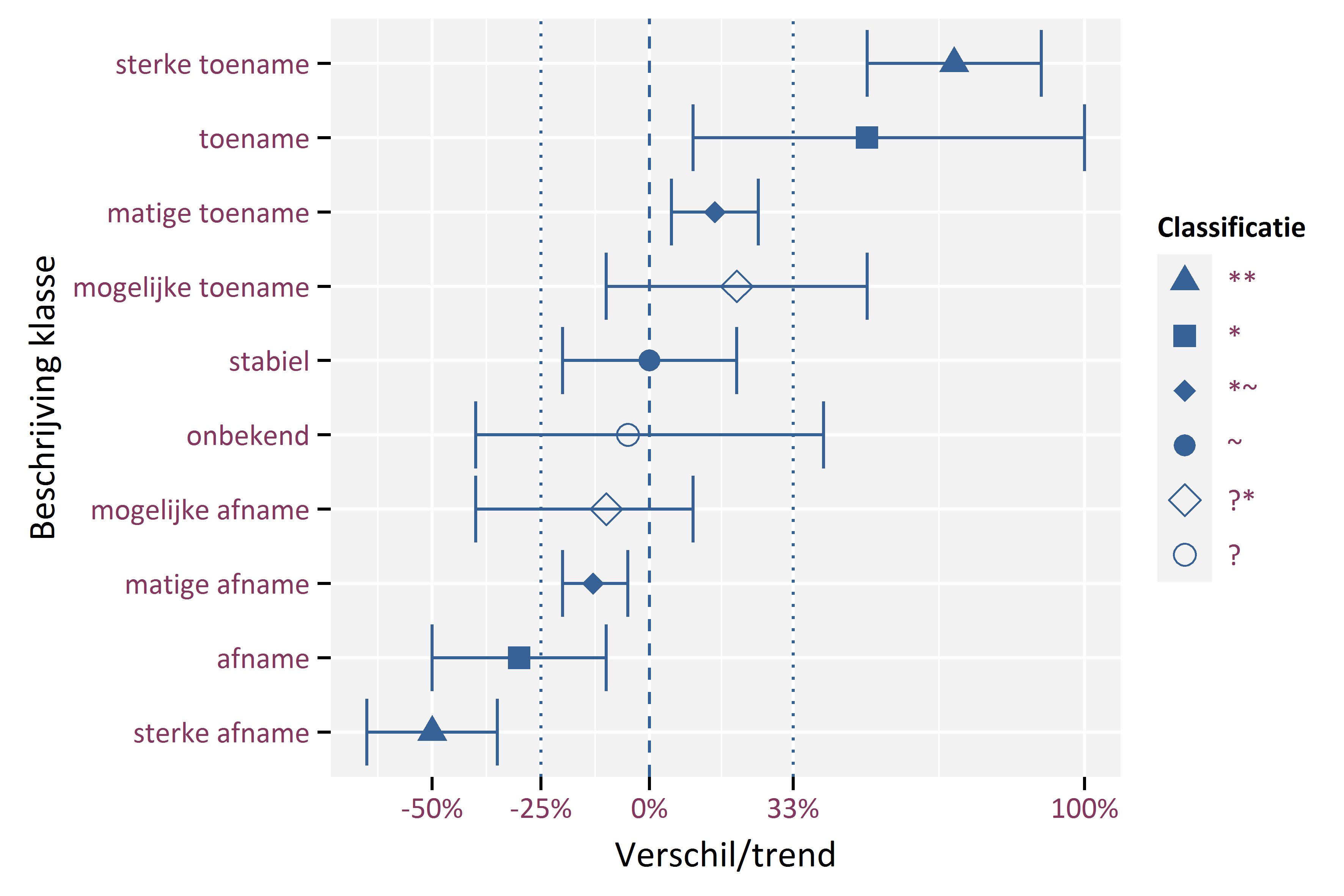
Figuur 5.2: Classificatie van trends of verschillen
Een van de voordelen van dit systeem is het onderscheid tussen ‘stabiel’ en ‘onbekend’ wanneer er geen significante trend is. In het eerste geval weten we met zekerheid dat er geen sterke toename of afname is. In het tweede geval is de onzekerheid dermate groot dat we geen enkele conclusie kunnen trekken op basis van de data.
Ook de klassen ‘mogelijke toename’ en ‘mogelijke afname’ geven een meerwaarde. Zeker omdat we voor de soortenmeetnetten nog maar enkele jaren aan het meten zijn waardoor de onzekerheid op de schattingen vrij groot is. Via deze bijkomende klassen verkrijgen we al een indicatie van de trendrichting ook al kunnen we nog geen significante trend detecteren.
| Code | Klasse | Beschrijving |
|---|---|---|
| ++ | sterke toename | Significante positieve trend, significant hoger dan bovenste drempelwaarde |
| + | toename | Significante positieve trend, maar geen significant verschil met bovenste drempelwaarde |
| +~ | matige toename | Significante positieve trend, significant lager dan bovenste drempelwaarde |
| ~ | stabiel | Geen significante trend, significant hoger dan onderste drempelwaarde en lager dan bovenste drempelwaarde |
| -~ | matige afname | Significante negatieve trend, significant hoger dan onderste drempelwaarde |
| - | afname | Significante negatieve trend, maar geen significant verschil met onderste drempelwaarde |
| -- | sterke afname | Significante negatieve trend, significant hoger dan onderste drempelwaarde |
| ?+ | mogelijke toename | Geen significante trend, significant hoger dan onderste drempelwaarde |
| ?- | mogelijke afname | Geen significante trend, significant lager dan bovenste drempelwaarde |
| ? | onbekend | Geen significante trend, geen significant verschil met bovenste en onderste drempelwaarde |
5.3 Voorstelling resultaten
We tonen de resultaten voor Kempense heidelibel, Maanwaterjuffer en Gevlekte witsnuitlibel. Dit zijn drie soorten die via het veldprotocol ‘gebiedstelling’ geteld worden en waarvan het meetnet in 2016 is opgestart. Voor andere soorten zullen de resultaten op een gelijkaardige manier voorgesteld worden.
5.3.1 Modelschatting voor maximum (getelde) aantal per jaar
Figuur 5.3 toont de moddelschatting en betrouwbaarheidsinterval voor het maximum getelde aantal binnen het telseizoen. Dit komt dus overeen met de piek van de zwarte lijn in Figuur 5.1.
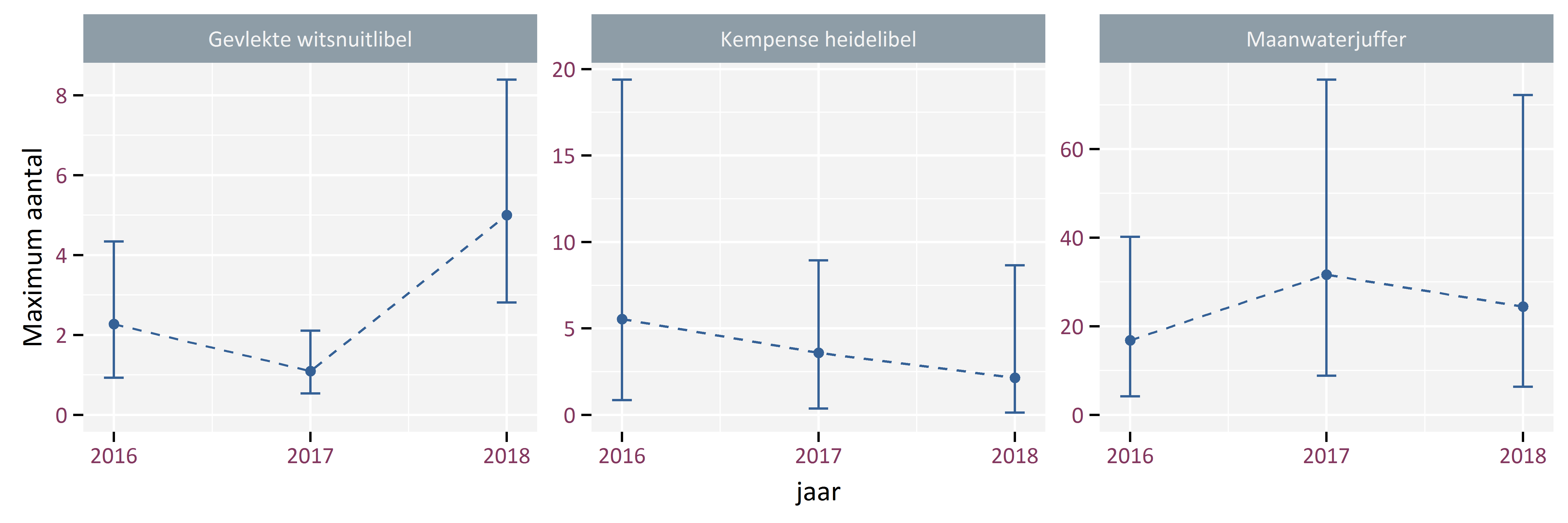
Figuur 5.3: Modelschatting voor het maximum getelde aantal voor Gevlekte witsnuitlibel, Kempense heidelibel en Maanwaterjuffer
5.3.2 Jaarlijkse index met 2016 als referentiejaar
Figuur 5.4 toont de jaarlijkse index met 2016 als referentiejaar. De index voor het jaar 2016 is gelijk aan 100.
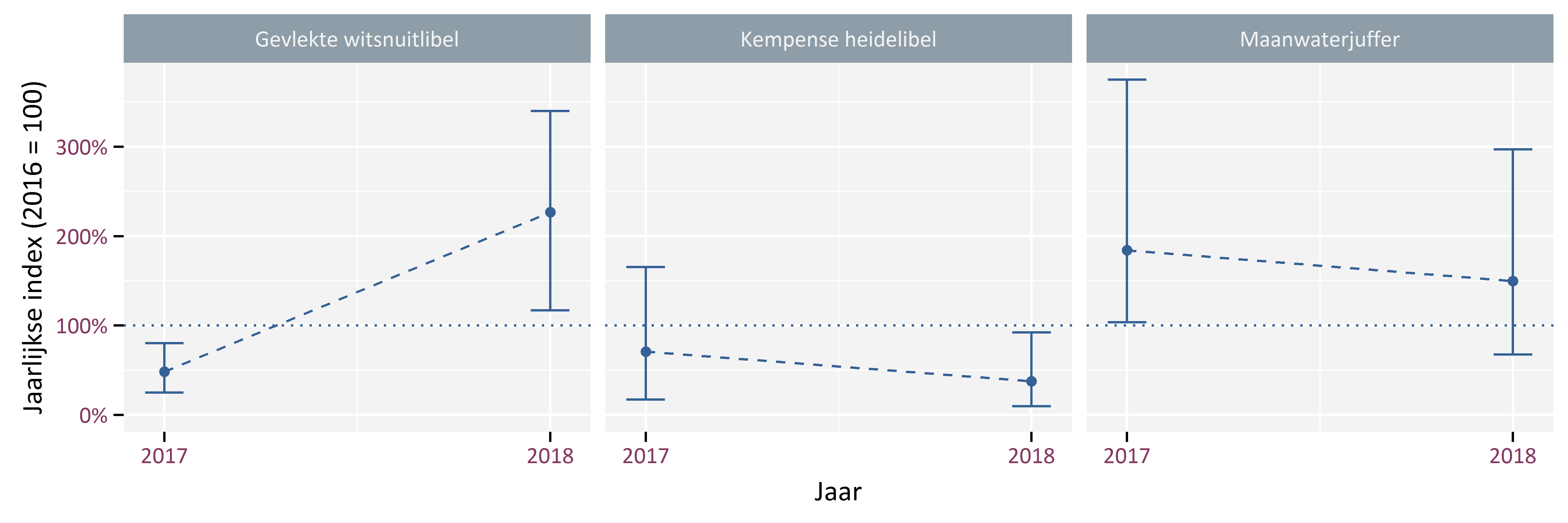
Figuur 5.4: Jaarlijkse index met 2016 als referentiejaar voor Gevlekte witsnuitlibel, Kempense heidelibel en Maanwaterjuffer
5.3.3 Verschillen tussen de jaren
Ook andere jaren kunnen als referentiejaar gebruikt worden. Om alle combinaties te visualiseren stellen we Figuur 5.5 voor met in de y-as het referentiejaar en in de x-as het jaar dat vergeleken wordt met het referentiejaar. De symbolen tonen het type verschillen tussen de jaren volgens het classificatiesysteem in Figuur 5.2 en Tabel 5.1. Een gearceerde driehoek (**) kan dus zowel een sterke toename (++) als een sterke afname (--) betekenen. De kleur geeft de richting en de grootte van de verandering aan. We zien bijvoorbeeld voor de Gevlekte witsnuitlibel in 2018 een sterke toename t.o.v. 2017. Dit wordt weergegeven via een blauw gearceerde driehoek. Als we 2017 vergelijken t.o.v. 2018 als referentiejaar, dan krijgen we uiteraard hetzelfde resultaat maar dan in de andere richting (een oranje gearceerde driehoek).
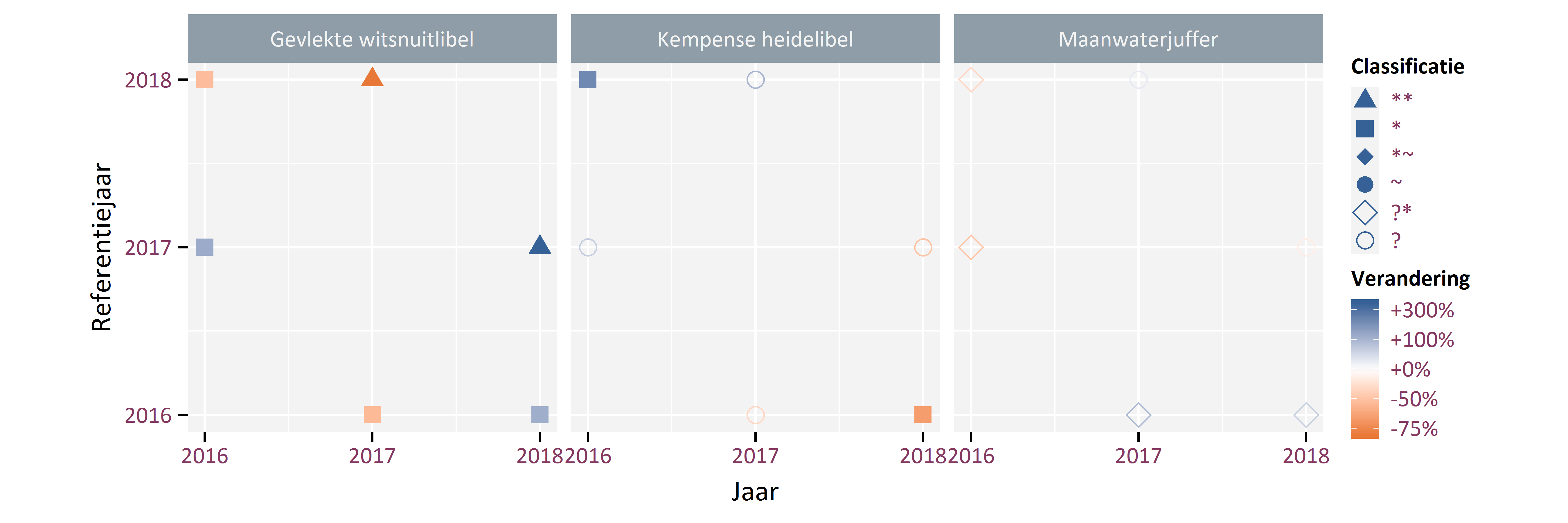
Figuur 5.5: Verschillen tussen de jaren voor Gevlekte witsnuitlibel, Kempense heidelibel en Maanwaterjuffer, met in de y-as het referentiejaar en in de y-as het jaar dat vergelijken wordt met het referentiejaar
5.3.4 Gemiddelde jaarlijkse trend
Figuur 5.6 toont de gemiddelde jaarlijkse trend over de periode 2016-2018. Om het type trend te bepalen gebruiken we hier een jaarlijkse trend van -13.4% als onderste drempelwaarde en van 15.3 % als bovenste drempelwaarde. Beide drempelwaarden komen overeen met eenzelfde relatief effect: (100 - 13.4)/100 = 100/(100 + 15.3). Over de volledige trendperiode (3 jaar) komt dit overeen met een respectievelijk een afname van -25% en een toename van +33%.
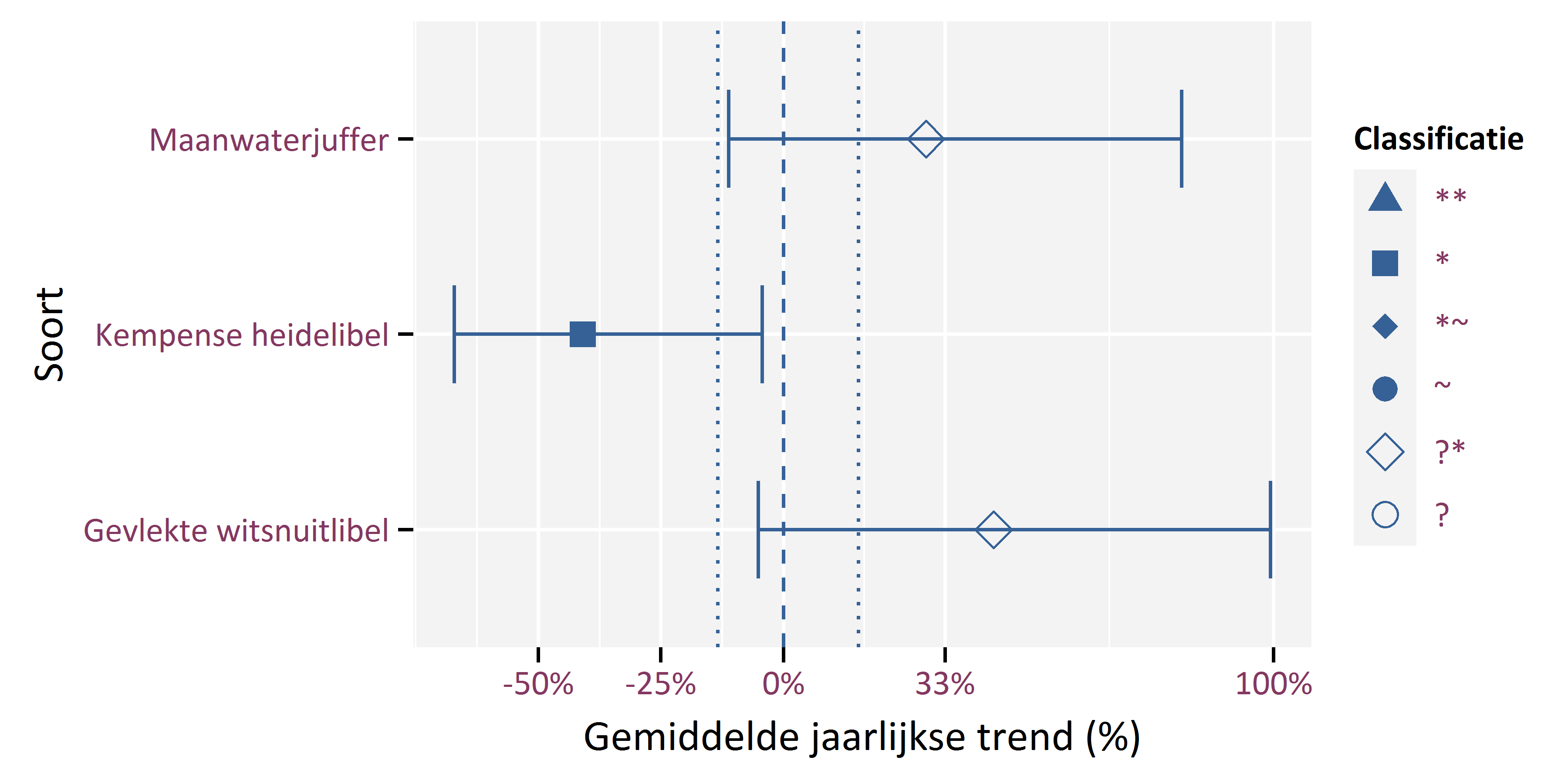
Figuur 5.6: Gemiddelde jaarlijkse trend over de periode 2016-2018 voor Gevlekte witsnuitlibel, Kempense heidelibel en Maanwaterjuffer
In Tabel 5.2 geven we een overzicht van de jaarlijkse trends en duiden we ook aan of de trend al dan niet lineair is. Een lineaire trend betekent dat de jaarlijkse daling of stijging relatief constant is. Bij een niet-lineaire trend fluctueren de aantallen sterk jaar per jaar, maar hebben we gemiddeld gezien over de hele tijdsperiode wel een stijging of een daling. Het onderscheid tussen een lineaire en een niet-lineaire trend maken we op basis van de WAIC, een maat die aangeeft in hoeverre het model overeenkomt met de data (de model fit). Hoe lager de WAIC, hoe beter de model fit. Als het model voor de lineaire trend een lagere WAIC heeft dan het model voor het verschil tusssen de jaren, gaan we uit van een lineaire trend. In het andere geval gaan we dus uit van een niet-lineaire trend.
| soort | klasse | trend | type trend |
|---|---|---|---|
| Gevlekte witsnuitlibel | ?+ | +43% (-5%; +99%) | Niet lineair |
| Maanwaterjuffer | ?+ | +29% (-11%; +81%) | Niet lineair |
| Kempense heidelibel | - | -41% (-67%; -4%) | Lineair |